при a = -0.785 рад.
b = 1.0 рад.
wy2 = 2 рад/с.
wy2' = -3 рад/с2.
wz2 = -2 рад/с.
wz2' = 3 рад/с2.
wx0 = wz0 = 1 рад/c.
wx0' = wz0' = - 0.2 рад/c2.
wy0 = 0.167 рад/c.
wy0' = 0.167 рад/c2.
Вклад Мцб в суммарный возмущающий момент составил:
Мцб
![]() К
= Ч
100 % = 3.02 %
К
= Ч
100 % = 3.02 %
Мy1ин + Мцб
Исследование влияния нежесткостей элементов гиростабилизатора на его устойчивость.
Анализ устойчивости ГС с нежесткими наружной рамой, креплением статора двигателя стабилизации к раме, с нежесткими редуктором и связью платформы с объектом стабилизации, проводим основываясь на следующей физической модели:
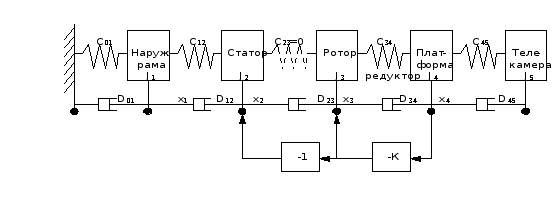
Рис. 1.
здесь Ji - момент инерции i-го элемента;
Ci,j - коэффициент упругости;
Di,j - коэфф. демпфирования между i и j
элементами;
K - коэффициент передачи цепи обратной
связи.
Оценку влияния каждого из входящих в модель элементов (Ji,Ci,j,Di,j) выполняем на основе анализа поведения ЛАХ разомкнутой системы, при вариациях Ji,Ci,j,Di,j.
Уравнения движения каждого из элементов модели в общем виде могут быть представлены следующим образом:
JiЧxi''+Di-1,iЧ(xi'-xi-1')-Di,i+1Ч(xi+1'-xi')+Ci-1,iЧ (xi-xi-1)-Ci,i+1Ч(xi+1 - xi) = Мi (1)
где Мi - внешний момент действующий на i-й элемент;
xi,xi', xi''- перемещение, скорость и ускорение i-го
элемента.
Расписав уравнение (1) для каждого элемента, получим следующюю систему уравнений движения модели:
J1Чx1''+D01Ч(x1'-x0')-D12Ч(x2'-x1')+C01Ч(x1-x0)-C12Ч(x2-x1)= М1
J2Чx2''+D12Ч(x2'-x1')-D23Ч(x3'-x2')+C12Ч(x2-x1)-C23Ч(x3-x2)= М2
J3Чx3''+D23Ч(x3'-x2')-D34Ч(x4'-x3')+C23Ч(x3-x2)-C34Ч(x4-x3)= М3 (2)
J4Чx4''+D34Ч(x4'-x3')-D45Ч(x5'-x4')+C34Ч(x4-x3)-C45Ч (x5-x4)= М4
J5Чx5''+D45Ч(x5'-x4')-D56Ч(x6'-x5')+C45Ч(x5-x4)-C56Ч(x6-x5)= М5
Раскрыв в (2) скобки и преобразовав получаем следующий вид уравнений движения модели.
-D01Чx0'-C01Чx0+J1Чx1''+(D01+D12)Чx1'+(C01+C12)Чx1-D34Чx2'-
-C12Чx2= М1
-D12Чx1'-C12Чx1+J2Чx2''+(D23+D12)Чx2'+(C12+C23)Чx2-D23Чx3'-
-C23Чx3= М2
-D23Чx2'-C23Чx2+J3Чx3''+(D23+D34)Чx3'+(C23+C34)Чx3-D34Чx4'-
-C34Чx4=М3 (3)
-D34Чx3'-C34Чx3+J4Чx4''+(D34+D45)Чx4'+(C34+C45)Чx4-D45Чx5'-
-C45Чx5= М4
-D45Чx4'-C45Чx4+J5Чx5''+(D45+D56)Чx5'+(C45+C56)Чx5-D56Чx6'-
-C56Чx6= М5
Переписав (3) в операторной форме получаем уравнения движения модели в следующем виде.
-(D01Чs+C01)Чx0+(J1Чs2+(D01+D12)Чs+(C01+C12))Чx1 -
-(D12Чs+C12)Чx2= М1
-(D12Чs+C12)Чx1+(J2Чs2+(D12+D23)Чs+(C12+C23))Чx2-
-(D23Чs+C23)Чx3= КЧx4
-(D23Чs+C23)Чx2+(J3Чs2+(D23+D34)Чs+(C23+C34))Чx3-
-(D34Чs+C34)Чx4=-КЧx4
-(D34Чs+C34)Чx3+(J4Чs2+(D34+D45)Чs+(C34+C45))Чx4-
-(D45Чs+C45)Чx5= М4 (4)
-(D45Чs+C45)Чx4+(J5Чs2+(D45+D56)Чs+(C45+C56))Чx5-
-(D56Чs+C56)Чx6= М5
Для нахождения передаточной функции разомкнутой системы по управляющему воздействию Wp(s) составим два определителя: главный - D, и характеризующий входное воздействие D1, с учетом того, что x0=0; D56=0; C56=0; C23=0.
![]()
![]()
a11 a12 0 0 0
a21 a22 a23 0 0
D= 0 a32 a33 a34 0 (5)
0 0 a43 a44 a45
0 0 0 a54 a55
где a11 = J1Чs2+(D01+D12)Чs+C01+C12
a12 = -D12Чs-C12
a21 = a12
a22 = J2Чs2+(D12+D23)Чs+C12
a23 = -D23Чs
a32 = a23
a33 = J3Чs2+(D23+D34)Чs+C34
a34 = -D34Чs-C34
a43 = a34
a44 = J4Чs2+(D34+D45)Чs+C34+C45
a45 = -D45Чs-C45
a54 = a45
a55 = J5Чs2+D45Чs+C45
![]()
![]() a11 a12 0 0 0
a11 a12 0 0 0
a21 a22 a23 -KЧx4 0
D1= 0 a32 a33 KЧx4 0 (6)
0 0 a43 0 a45
0 0 0 0 a55
Передаточная функция разомкнутой системы определяется как:
![]() D1 -KЧ(b7Чs7+....+b1Чs+b0)Чx4
D1 -KЧ(b7Чs7+....+b1Чs+b0)Чx4
![]()
![]() Wp(s)
= = (7)
Wp(s)
= = (7)
![]() DЧx4
sЧ(a9Чs9+....+a1Чs+a0)Чx4
DЧx4
sЧ(a9Чs9+....+a1Чs+a0)Чx4
Коэффициенты ai, bi полиномов числителя и знаменателя передаточной функции Wp(s) выражаются через параметры элементов модели следующим образом:
(8)
a9=J1J2J3J4J5
a8=D01J2J3J4J5+D12J3J4J5(J1+J2)+J1(D23J4J5(J2+J3)+J2(D34J5(J3+J4)+D45J3(J4+J5)))
a7=C01J2J3J4J5+C12J3J4J5(J1+J2)+C34J1J2(J3J5+J4J5)+C45J1J2J3(J4+J5)+D01(D12J3J4J5+D23J4J5(J2+J3)+J2(D34J5(J3+J4)+D45J3(J4+J5)))+D12(D23J4J5(J1+J2+J3)+(J1+J2)(D34J5(J3+J4)+D45J3(J4+J5)))+J1(D23(D34J5(J2+J3+J4)+D45(J4+J5)(J2+J3))+D34D45J2(J3+J4+J5))
a6=C01(D12J3J4J5+D23J4J5(J2+J3)+J2(D34J5(J3+J4)+D45J3(J4+J5)))+C12(D01J3J4J5+D23J4J5(J1+J2+J3)+(J1+J2)(D34J5(J3+J4)+D45J3(J4+J5)))+C34(D01J2(J3J5+J4J5)+D12J5(J3+J4)(J1+J2)+J1(D23J5(J2+J3+J4)+D45J2(J3+J4+J5)))+C45(D01J2J3(J4+J5)+D12J3(J4+J5)(J1+J2)+J1(D23(J4+J5)(J2+J3)+D34J2(J3+J4+J5)))+D01(D12(D23J4J5+D34(J3J5+J4J5)+D45J3(J4+J5))+D23(D34(J2J5+J3J5+J4J5)+D45(J4+J5)(J2+J3))+D34D45J2(J3+J4+J5))+D12(D23(D34(J1J5+J2J5+J3J5+J4J5)+D45(J4+J5)(J1+J2+J3))+D34D45(J3+J4+J5)(J1+J2))+D23D34D45J1(J2+J3+J4+J5)
a5=C01(C12J3J4J5+C34J2(J3J5+J4J5)+C45J2J3(J4+J5)+D12(D23J4J5+D34(J3J5+J4J5)+D45J3(J4+J5))+D23(D34(J2J5+J3J5+J4J5)+D45(J4+J5)(J2+J3))+D34D45J2(J3+J4+J5))+C12(C34J5(J3+J4)(J1+J2)+C45J3(J4+J5)(J1+J2)+D01(D23J4J5+D34(J3J5+J4J5)+D45J3(J4+J5))+D23(D34(J1J5+J2J5+J3J5+J4J5)+D45(J4+J5)(J1+J2+J3))+D34D45(J3+J4+J5)(J1+J2))+C34(C45J1J2(J3+J4+J5)+D01(D12(J3J5+J4J5)+D23(J2J5+J3J5+J4J5)+D45J2(J3+J4+J5))+D12(D23(J1J5+J2J5+J3J5+J4J5)+D45(J3+J4+J5)(J1+J2))+D23D45J1(J2+J3+J4+J5))+C45(D01(D12J3(J4+J5)+D23(J2(J4+J5)+J3(J4+J5))+D34J2(J3+J4+J5))+D12(D23(J1(J4+J5)+J2(J4+J5)+J3(J4+J5))+D34(J3+J4+J5)(J1+J2))+D23D34J1(J2+J3+J4+J5))+D01(D12(D23(D34J5+D45(J4+J5))+D34D45(J3+J4+J5))+D23D34D45(J2+J3+J4+J5))+D12D23D34D45(J1+J2+J3+J4+J5)
a4=C01(C12(D23J4J5+D34(J3J5+J4J5)+D45J3(J4+J5))+C34(D12(J3J5+J4J5)+D23(J2J5+J3J5+J4J5)+D45J2(J3+J4+J5))+C45(D12J3(J4+J5)+D23(J2(J4+J5)+J3(J4+J5))+D34J2(J3+J4+J5))+D12(D23(D34J5+D45(J4+J5))+D34D45(J3+J4+J5))+D23D34D45(J2+J3+J4+J5))+C12(C34(D01(J3J5+J4J5)+D23(J1J5+J2J5+J3J5+J4J5)+D45(J3+J4+J5)(J1+J2))+C45(D01J3(J4+J5)+D23(J1(J4+J5)+J2(J4+J5)+J3(J4+J5))+D34(J3+J4+J5)(J1+J2))+D01(D23(D34J5+D45(J4+J5))+D34D45(J3+J4+J5))+D23D34D45(J1+J2+J3+J4+J5))+C34(C45(D01J2(J3+J4+J5)+D12(J1(J3+J4+J5)+J2(J3+J4+J5))+D23J1(J2+J3+J4+J5))+D01(D12(D23J5+D45(J3+J4+J5))+D23D45(J2+J3+J4+J5))+D12D23D45(J1+J2+J3+J4+J5))+C45(D01(D12(D23(J4+J5)+D34(J3+J4+J5))+D23D34(J2+J3+J4+J5))+D12D23D34(J1+J2+J3+J4+J5))+D01D12D23D34D45
a3=C01(C12(C34(J3J5+J4J5)+C45J3(J4+J5)+D23(D34J5+D45(J4+J5))+D34D45(J3+J4+J5))+C34(C45J2(J3+J4+J5)+D12(D23J5+D45(J3+J4+J5))+D23D45(J2+J3+J4+J5))+C45(D12(D23(J4+J5)+D34(J3+J4+J5))+D23D34(J2+J3+J4+J5))+D12D23D34D45)+C12(C34(C45(J1(J3+J4+J5)+J2(J3+J4+J5))+D01(D23J5+D45(J3+J4+J5))+D23D45(J1+J2+J3+J4+J5))+C45(D01(D23(J4+J5)+D34(J3+J4+J5))+D23D34(J1+J2+J3+J4+J5))+D01D23D34D45)+C34(C45(D01(D12(J3+J4+J5)+D23(J2+J3+J4+J5))+D12D23(J1+J2+J3+J4+J5))+D01D12D23D45)+C45D01D12D23D34
a2=C01(C12(C34(D23J5+D45(J3+J4+J5))+C45(D23(J4+J5)+D34(J3+J4+J5))+D23D34D45)+C34(C45(D12(J3+J4+J5)+D23(J2+J3+J4+J5))+D12D23D45)+C45D12D23D34)+C12(C34(C45(D01(J3+J4+J5)+D23(J1+J2+J3+J4+J5))+D01D23D45)+C45D01D23D34)+C34C45D01D12D23
a1=C01(C12(C34(C45(J3+J4+J5)+D23D45)+C45D23D34)+C34C45D12D23)+C12C34C45D01D23
a0=C01C12C34C45D23
b7=D34J1J2J5
b6=(C34J1J2J5+D34(D01J2J5+D12J5(J1+J2)+D45J1J2))
b5=(C01D34J2J5+C12D34J5(J1+J2)+C34(D01J2J5+D12J5(J1+J2)+D45J1J2)+C45D34J1J2+D34(D01(D12J5+D45J2)+D12D45(J1+J2)))
b4=(C01(C34J2J5+D12D34J5+D34D45J2)+C12(C34J5(J1+J2)+D01D34J5+D34D45(J1+J2))+C34(C45J1J2+D01(D12J5+D45J2)+D12D45(J1+J2))+C45D34(D01J2+D12(J1+J2))+D01D12D34D45)
b3=(C01(C12D34J5+C34(D12J5+D45J2)+C45D34J2+D12D34D45)+C12(C34(D01J5+D45(J1+J2))+C45D34(J1+J2)+D01D34D45)+C34(C45(D01J2+D12(J1+J2))+D01D12D45)+C45D01D12D34)
b2=(C01(C12(C34J5+D34D45)+C34(C45J2+D12D45)+C45D12D34)+C12(C34(C45(J1+J2)+D01D45)+C45D01D34)+C34C45D01D12)
b1=(C01(C12(C34D45+C45D34)+C34C45D12)+C12C34C45D01)
b0=C01C12C34C45
Представить передаточную функцию Wp(s) в виде произведения полиномов не выше второго порядка в числителе и знаменателе Wp(s) в аналитическом виде не представляется возможным даже теоретически, т.к. вид корней характеристических полиномов ai,bi, а, следовательно, и вид разложения на полиномы не выше второго порядка, зависит от численных значений параметров элементов модели. Поэтому исследование влияния элементов модели на устойчивость ГС проводилось численно, путем нахождения корней характеристических полиномов для каждого частного случая. Далее по полученным корням определялись полиномы не выше второго порядка по которым и строилась ЛАХ разомкнутой системы.
Все математические операции проводилось с использованием пакета “MATHCAD” с помощью которого численно определялись корни полиномов в передаточной функции разомкнутой системы Wp(s), зная которые можно представить Wp(s) в виде последовательного соединения элементарных звеньев. Это выполняется следующим образом. Пусть полиномы числителя и знаменателя Wp(s) имеют корни lai, lbi соответственно. Эти корни могут быть нулевыми, действительными и комплексно сопряженными. Каждый нулевой корень знаменателя lai=0 обеспечивает появление в составе Wp(s) интегрирующего звена Wi(s)= 1/s, соответственно lbi=0 отвечает за появление чисто дифференцирующего звена с Wi(s)= s. Каждый из действительных корней lai, lbi приносит в числитель или знаменатель соответственно выражение вида (TiЧs+1)Ч(1/Ti), где Ti=1/li , что соответствует появлению апериодических и дифференцирующих звеньев в составе Wp(s). Каждая пара комплексно сопряженных корней li, li* в составе числителя или знаменателя передаточной функции отвечает за появление в числителе или знаменателе соответственно выражений вида (Ti2 Ч s2 +2ЧxiЧTiЧs +1)Ч(1/Ti2), где Ti=1 / |li| , xi=Re(li) / |li|. Таким образом, зная корни полиномов числителя и знаменателя передаточной функции можно представить её в виде:
П(si)ЧП(TgЧs+1)ЧП( Tn2 Ч s2 +2ЧxnЧTnЧs +1)
![]() Wp(s)
= k Ч
kw Ч
(9)
Wp(s)
= k Ч
kw Ч
(9)
П(sj)ЧП(TkЧs+1)ЧП( Tm2 Ч s2 +2ЧxmЧTmЧs +1)
П(1/Ti) Ч П(1/Ti2)
![]() где
kw =
где
kw =
П(1/Ti) Ч П(1/Ti2)
Для численных расчетов примем базовые параметры модели характерными для ГС данного типа, которые равны следующим значениям:
J1 = 0.25 кгЧм2 C01 = 1Ч103 НЧм/рад. D01=0.001 НЧмЧс
J2 = 0.03 кгЧм2 C12 = 1Ч103 НЧм/рад. D12=0.001 НЧмЧс
J3 = 0.01 кгЧм2 C23 = 0 D23=0.1 НЧмЧс
J4 = 0.15 кгЧм2 C34 =1Ч104 НЧм/рад. D34=0.001 НЧмЧс
J5 = 1 кгЧм2 C45 =1Ч103 НЧм/рад. D45=0.01 НЧмЧс
К = 1000
Рассмотрим следующие варианты модели:
1) ГС с “жесткими” рамами и редуктором.
Начальные параметры модели принимают следующие знечения:
J1 = 0.25 кгЧм2 C01 = 1Ч1020 НЧм/рад. D01= 0.001 НЧмЧс
J2 = 0.03 кгЧм2 C12 = 1Ч1020 НЧм/рад. D12= 0.001 НЧмЧс
J3 = 0.01 кгЧм2 C23 = 0 D23=0.1 НЧмЧс
J4 = 0.15 кгЧм2 C34 =1Ч1020 НЧм/рад. D34=0.001 НЧмЧс
J5 = 1 кгЧм2 C45 =1Ч1020 НЧм/рад. D45=0.01 НЧмЧс
К = 1000
Варьируем D23 = 0.01 ... 1 HЧмЧс
Передаточная функция при этом имеет вид:
k Ч kw
![]() Wp(s)= (10)
Wp(s)= (10)
s Ч (TЧs+1)
Значения постоянной времени Т, w, kw приведены в Табл.1.
Табл.1.
| D23 | T |
w=1/T |
kw |
| 0.01 | 116 | 0.0086 | 150 |
| 0.1 | 11.6 | 0.086 | 15 |
| 1 | 1.16 | 0.86 | 1.5 |
| 10 | 0.116 | 8.6 | 0.15 |
Т.о. ЛАХ модели с бесконечно жесткими пружинами соответствует ЛАХ идеализированного индикаторного ГС. Постоянная времени Т апериодического звена апроксимируется формулой:
J3 +J4 +J5
![]() Т= (11)
Т= (11)
D23
2) ГС с “нежестким” редуктором.
Начальные параметры модели:
J1 = 0.25 кгЧм2 C01 = 1Ч1020 НЧм/рад. D01= 0.001 НЧмЧс
J2 = 0.03 кгЧм2 C12 = 1Ч1020 НЧм/рад. D12= 0.001 НЧмЧс
J3 = 0.01 кгЧм2 C23 = 0 D23=0.1 НЧмЧс
J4 = 0.15 кгЧм2 C34 =1Ч104 НЧм/рад. D34=0.001 НЧмЧс
J5 = 1 кгЧм2 C45 =1Ч1020 НЧм/рад. D45=0.01 НЧмЧс
К = 1000
Варьируем нежесткость редуктора С34=103 ... 107 HЧм/рад.
Передаточная функция при этом имеет вид:
k Ч kw
![]() Wp(s)= (12)
Wp(s)= (12)
s Ч (T1Чs+1)Ч( T22 Ч s2 +2Чx2ЧT2Чs +1)
Значения постоянных времени Т1, Т2, соответствующие им частоты “излома” ЛАХ w1, w1, удельный коэффициент демпфирования x2 и коэффициент передачи модели kw приведены в Табл.2. и Табл.3.
Табл.2.
| C34 | T1 |
w1 |
T2 |
w2 |
x2 |
kw |
| 103 | 24.25 | 0.04 | 0.0031 | 323 | 0.016 | 31.36 |
| 104 | 24.25 | 0.04 | 0.001 | 103 | 0.005 | 31.36 |
| 105 | 24.25 | 0.04 |
3.1Ч10-4 |
3.23 | 0.0016 | 31.36 |
| 106 | 24.25 | 0.04 |
1Ч10-4 |
104 | 0.0005 | 31.36 |
Как видно из Табл.2. нежесткость редуктора влияет только на расположение колебательного звена на оси частот (Т2, w2) и коэффициент демпфирования в этом звене (x2).
Влияние демпфирования в редукторе на поведение ЛАХ определяем варьируя D34=0.001 ... 0.1 НЧмЧс (при С34=104 = const.).
Табл.3.
| D34 | T1 |
w1 |
T2 |
w2 |
x2 |
kw |
| 0.0001 | 25.9 | 0.039 | 0.001 | 103 | 0.0049 | 334.8 |
| 0.001 | 24.25 | 0.04 | 0.001 | 103 | 0.005 | 31.36 |
| 0.01 | 14.86 | 0.067 | 0.001 | 103 | 0.0054 | 1.92 |
| 0.1 | 11.6 | 0.086 | 0.001 | 103 | 0.01 | 0.15 |
Как видно из Табл.3., изменение демпфирования в редукторе влияет не только на коэффициент демпфирования в колебательном звене, но и на расположение на оси частот апериодического звена (Т1), и на коэффициент передачи модели.
3) ГС с “нежесткой” связью платформы со стабилизируемым объектом (телекамерой).
Исходные параметры модели:
J1 = 0.25 кгЧм2 C01 = 1Ч1020 НЧм/рад. D01= 0.001 НЧмЧс
J2 = 0.03 кгЧм2 C12 = 1Ч1020 НЧм/рад. D12= 0.001 НЧмЧс
J3 = 0.01 кгЧм2 C23 = 0 D23=0.1 НЧмЧс
J4 = 0.15 кгЧм2 C34 =1Ч1020 НЧм/рад. D34=0.001 НЧмЧс
J5 = 1 кгЧм2 C45 =1Ч103 НЧм/рад. D45=0.01 НЧмЧс
К = 1000
Варьируем С45 = 102 ... 106 HЧм/рад.
Передаточная функция при этом имеет вид:
k Ч kwЧ( T32 Ч s2 +2Чx3ЧT3Чs +1)
![]() Wp(s)= (13)
Wp(s)= (13)
s Ч (T1Чs+1)Ч( T22 Ч s2 +2Чx2ЧT2Чs +1)
Влияние жесткости крепления стабилизируемого объекта к платформе на передаточную функцию Wp(s) приведено в Табл.4.
Табл.4.
| C45 |
T1 (w1) |
T2 (w2) |
x2 |
T3 (w3) |
x3 |
kw |
| 102 | 11.6 (0.086) | 0.037(27) | 0.011 | 0.1 (10) |
5Ч10-4 |
15 |
| 103 | 11.6 (0.086) | 0.012(85) | 0.0036 | 0.032(31.3) |
1.6Ч10-4 |
15 |
| 104 | 11.6 (0.086) | 0.0037(270) | 0.0011 | 0.01(100) |
5Ч10-5 |
15 |
| 105 | 11.6 (0.086) |
1.2Ч10-3(850) |
0.00036 |
3.2Ч10-3(313) |
1.6Ч10-5 |
15 |
Влияние демпфирования в креплении стабилизируемого объекта к платформе на передаточную функцию Wp(s) приведено в Табл.5. Коэффициент демпфирования изменяется в пределах D45=0.001 ... 0.1 НЧмЧс, при постоянной жесткости крепления объекта к платформе равной C45=1000 HЧм/рад =const.
Табл.5.
| D45 |
T1 (w1) |
T2 (w2) |
x2 |
T3 (w3) |
x3 |
kw |
| 0.001 | 11.6 (0.086) | 0.012(85) | 0.0032 | 0.032 (31.3) |
2.7Ч10-14 |
15 |
| 0.01 | 11.6 (0.086) | 0.012(85) | 0.0036 | 0.032(31.3) |
1.6Ч10-4 |
15 |
| 0.1 | 11.6 (0.086) | 0.012(85) | 0.0074 | 0.032(31.3) |
1.6Ч10-3 |
15 |
Как видно из Табл.4. и 5., нежесткость крепления объекта к платформе вызывает появление в составе ЛАХ двух звеньев: колебательного и антиколебательного, причем антиколебательное звено всегда расположено в области более низких частот, чем колебательное. Это влечет появление в ЛАХ участка с наклоном в 0 Дб/дек., который в случае его расположения до частоты среза, увеличивает частоту среза, что вызывает трудности в технической реализации такой системы стабилизации. Демпфирование в креплении объекта к платформе влияет только на удельные коэффициенты демпфирования x2, x3 в колебательном и антиколебательном звеньях, причем особенно сильно изменяется x3.
4) ГС с “нежестким” креплением статора двигателя стабилизации к наружной раме (задняя нежесткость).
Параметры модели:
J1 = 0.25 кгЧм2 C01 = 1Ч1020 НЧм/рад. D01= 0.001 НЧмЧс
J2 = 0.03 кгЧм2 C12 = 1Ч103 НЧм/рад. D12= 0.001 НЧмЧс
J3 = 0.01 кгЧм2 C23 = 0 D23=0.1 НЧмЧс
J4 = 0.15 кгЧм2 C34 =1Ч1020 НЧм/рад. D34=0.001 НЧмЧс
J5 = 1 кгЧм2 C45 =1Ч1020 НЧм/рад. D45=0.01 НЧмЧс
К = 1000
Варьируем С12 = 102 ... 106 HЧм/рад.
Передаточная функция при этом имеет вид:
k Ч kwЧ( T32 Ч s2 +2Чx3ЧT3Чs +1)
![]() Wp(s)= (14)
Wp(s)= (14)
s Ч (T1Чs+1)Ч( T22 Ч s2 +2Чx2ЧT2Чs +1)
Варьируем С12 (при D12=0.001 НЧмЧс=const), результаты приведены в Табл.6.
Табл.6.
| C12 | T1 | T2 |
x2 |
T3 |
x3 |
kw |
| 102 | 11.6 | 0.017 | 0.03 | 0.017 | 0.0003 | 15 |
| 103 | 11.6 | 0.0055 | 0.0092 | 0.0055 |
9.1Ч10-5 |
15 |
| 104 | 11.6 | 0.0017 | 0.003 | 0.0017 |
2.9Ч10-5 |
15 |
| 105 | 11.6 | 0.00055 | .00092 | .00055 |
9.1Ч10-6 |
15 |
Варьируем D12 (при С12=1000 HЧм/рад = const.), результаты приведены в Табл.7.
Табл.7.
| D12 |
T1/w1 |
T2 / w2 |
x2 |
T3 / w3 |
x3 |
kw |
| 10-4 | 11.6 | 0.0055 | 0.0092 | 0.0055 |
8.3Ч10-14 |
15 |
| 10-3 | 11.6 | 0.0055 | 0.0092 | 0.0055 |
9.1Ч10-5 |
15 |
| 10-2 | 11.6 | 0.0055 | 0.01 | 0.0055 | 0.00091 | 15 |
Как видно из Табл.6, нежесткость крепления статора двигателя стабилизации к основанию, приводит к появлению в составе передаточной функции Wp(s) колебательного и антиколебательного звеньев с одинаковыми постоянными времени и различными коэффициентами демпфирования. Т.к. постоянные времени этих звеньев одинаковы, то наличие “задней” нежесткости никак не отражается на виде ЛАХ, однако различия этих звеньев в коэффициентах демпфирования влекут разную скорость “переключения” фазы в каждом звене, что вызывает появление незначительных по амплитуде выбросов на фазо-частотной характеристике.
5) ГС с “нежесткой” наружной рамкой.
Исходные параметры модели:
J1 = 0.25 кгЧм2 C01 = 1Ч103 НЧм/рад. D01= 0.001 НЧмЧс
J2 = 0.03 кгЧм2 C12 = 1Ч103 НЧм/рад. D12= 0.001 НЧмЧс
J3 = 0.01 кгЧм2 C23 = 0 D23=0.1 НЧмЧс
J4 = 0.15 кгЧм2 C34 =1Ч1020 НЧм/рад. D34=0.001 НЧмЧс
J5 = 1 кгЧм2 C45 =1Ч1020 НЧм/рад. D45=0.01 НЧмЧс
К = 1000
Варьируем С01,С12 = 102 ... 106 HЧм/рад.
Передаточная функция при этом имеет вид:
k Ч kwЧ( T42 Ч s2 +2Чx4ЧT4Чs +1) Ч( T52 Ч s2 +2Чx5ЧT5Чs +1)
![]() Wp(s)=
(14)
Wp(s)=
(14)
s Ч (T1Чs+1)Ч( T22 Ч s2 +2Чx2ЧT2Чs +1) Ч( T32 Ч s2 +2Чx3ЧT3Чs +1)
Вначале варьируем С01, при С12=const., результаты приведены в Табл.8.
Табл.8.
| C01 | T1 | T2 |
x2 |
T3 |
x3 |
T4 |
x4 |
T5 |
x5 |
kw |
| 102 | 11.6 | 0.0052 | 0.0078 | 0.053 | 0.0097 | 0.0052 | 0.0001 | 0.053 |
1.8 10-13 |
15 |
| 103 | 11.6 | 0.0051 | 0.0076 | 0.017 | 0.0037 | 0.0051 |
9.7 10-5 |
0.017 |
1.76 10-13 |
15 |
| 104 | 11.6 | 0.0062 | 0.0074 | 0.0044 | 0.0022 | 0.0044 |
5.7 10-5 |
0.0062 |
4.8 10-5 |
15 |
| 105 | 11.6 | 0.0055 | 0.0093 | 0.0016 |
9.4 10-6 |
0.0055 |
8.9 10-5 |
0.0016 |
4.37 10-13 |
15 |
Далее варьируем С12, при С01=const., результаты - в Табл.9.
Табл.9.
| C12 | T1 | T2 |
x2 |
T3 |
x3 |
T4 |
x4 |
T5 |
x5 |
kw |
| 102 | 11.6 | 0.0196 | 0.023 | 0.014 | 0.0069 | 0.0196 |
1.5 10-4 |
0.014 |
1.8 10-4 |
15 |
| 104 | 11.6 | 0.0016 | 0.0025 | 0.017 | 0.0031 | 0.0016 |
3.1 10-5 |
0.017 |
1.8 10-13 |
15 |
| 105 | 11.6 | .00052 | .00078 | 0.017 | 0.003 | .00052 |
0.9 10-5 |
0.017 |
1.8 10-13 |
15 |
Варьируя последовательно D01 и D12 выявляем степень их влияния на Ti, при С01=С12=1000 HЧм/рад = const. (Табл.10,11)
Табл.10.
| D01 |
T1/w1 |
T2 / w2 |
x2 |
T3 / w3 |
x3 |
T4 / w4 |
x4 |
T5 / w5 |
x5 |
kw |
| 10-4 | 11.6 | 0.0051 | 0.0076 | 0.0168 | 0.0037 | 0.0051 |
9.6Ч10-5 |
0.0168 |
2Ч 10-14 |
15 |
| 10-3 | 11.6 | 0.0051 | 0.0076 | 0.0168 | 0.0037 | 0.0051 |
9.7Ч10-5 |
0.0168 |
17Ч 10-14 |
15 |
| 10-2 | 11.6 | 0.0051 | 0.0076 | 0.0168 | 0.004 | 0.0051 |
11Ч10-5 |
0.0168 | .0003 | 15 |
| 10-1 | 11.6 | 0.0051 | 0.0076 | 0.0168 | 0.007 | 0.0051 |
23Ч10-5 |
0.0168 | .0003 | 15 |
Табл.11.
| D12 |
T1/w1 |
T2 / w2 |
x2 |
T3 / w3 |
x3 |
T4 / w4 |
x4 |
T5 / w5 |
x5 |
kw |
| 10-4 | 11.6 | 0.0051 | 0.0075 | 0.0168 | 0.0037 | 0.0051 |
1.1Ч10-5 |
0.0168 |
9Ч 10-6 |
15 |
| 10-2 | 11.6 | 0.0051 | 0.0084 | 0.0168 | 0.0037 | 0.0051 |
9.6Ч10-4 |
0.0168 |
2Ч 10-13 |
15 |
| 10-1 | 11.6 | 0.0051 | 0.017 | 0.0168 | 0.0037 | 0.0051 |
9.6Ч10-3 |
0.0168 |
4.2Ч 10-13 |
15 |
Как видно из таблиц 8 и 9, нежесткая “задняя” рамка (с двумя нежесткостями С01 и С12) приводит к появлению двух пар колебательных и антиколебательных звеньев, имеющих одинаковые постоянные времени, что приводит к их взаимной компенсации и, следовательно, влияние этих звеньев на вид ЛАХ практически отсутствует. Однако на ФЧХ будут присутствовать “выбросы” фазы, причина которых - различия коэффициентов демпфирования в компенсирующих друг друга колебательном и антиколебательном звеньях.
Вид ЛАХ в случае “нежесткой” задней рамки для исходных параметров модели следующий:
![]()

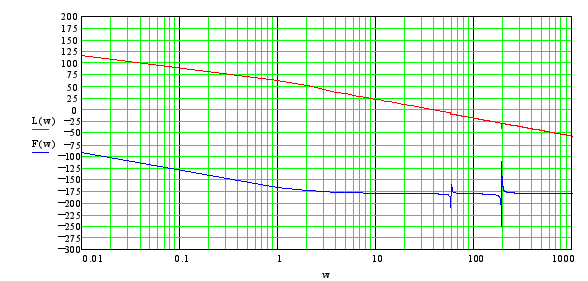
Таким образом, ЛАХ модели с базовыми параметрами:
J1 = 0.25 кгЧм2 C01 = 1Ч103 НЧм/рад. D01= 0.001 НЧмЧс
J2 = 0.03 кгЧм2 C12 = 1Ч103 НЧм/рад. D12= 0.001 НЧмЧс
J3 = 0.01 кгЧм2 C23 = 0 D23=0.1 НЧмЧс
J4 = 0.15 кгЧм2 C34 =1Ч104 НЧм/рад. D34=0.001 НЧмЧс
J5 = 1 кгЧм2 C45 =1Ч103 НЧм/рад. D45=0.01 НЧмЧс
К = 1000
имеет следующий вид.


![]()
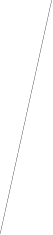
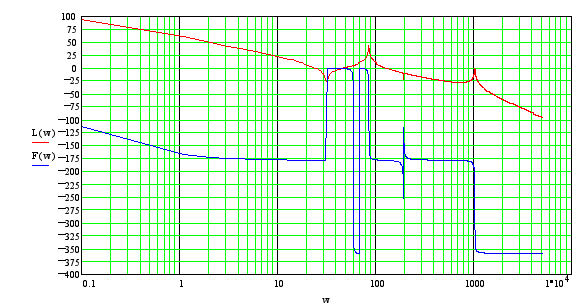
от нежесткости от “задней” от нежесткости
крепления объекта нежесткости редуктора
После предварительного рассмотрения влияния параметров модели на поведение ЛАХ, можно сделать следующие выводы:
1) В практических расчетах каждую нежесткость возможно рассматривать изолировано от других, т.к. при “типовых” параметрах ГС каждая такая нежесткость определяет звенья разнесенные по оси частот на некоторое расстояние и, поэтому, не влияющие друг на друга;
2) Из 1) следует, что влияние нежесткости редуктора на ЛАХ можно проводить основываясь на известных формулах, выведенных для более простой модели ГС, учитывающей только одну нежесткость редуктора;
3) В практических расчетах влиянием “задней” нежесткости можно пренебречь, т.к. она не изменяет вида ЛАХ из-за того, что колебательные и антиколебательные звенья взаимно компенсируют друг друга.
4) Нежесткость крепления объекта стабилизации к платформе вызывает появление на ЛАХ участка на котором характеристика “поднимается” на +40 Дб/дек. из-за появления в передаточной функции колебательного и антиколебательного звеньев, разнесенных по оси частот. Это не влияет на устойчивость системы стабилизации, но затрудняет её техническую реализацию из-за резко возрастающей частоты среза системы.
Таким образом, целесообразно подробнее рассмотреть влияние нежесткости крепления объекта стабилизации к платформе на поведние ЛАХ, при расположении чувствительного элемента на платформе и нежестком редукторе.
Для этого случая базовая модель имеет следующие значения параметров:
J1 = 0.25 кгЧм2 C01 = 1Ч1030 НЧм/рад. D01= 0.001 НЧмЧс
J2 = 0.03 кгЧм2 C12 = 1Ч1030 НЧм/рад. D12= 0.001 НЧмЧс
J3 = 0.01 кгЧм2 C23 = 0 D23=0.1 НЧмЧс
J4 = 0.15 кгЧм2 C34 =1Ч104 НЧм/рад. D34=0.001 НЧмЧс
J5 = 1 кгЧм2 C45 =1Ч103 НЧм/рад. D45=0.01 НЧмЧс
К = 1000
Варьируем следующие переменные: J3, J4, J5, C34, C45, D34, D45, при фиксированых значениях остальных параметров, равных базовым. Все единицы в СИ.
Передаточная функция для данной модели имеет вид:
k Ч kwЧ( T42 Ч s2 +2Чx4ЧT4Чs +1)
![]() Wp(s)=
(15)
Wp(s)=
(15)
s Ч (T1Чs+1)Ч( T22 Ч s2 +2Чx2ЧT2Чs +1) Ч( T32 Ч s2 +2Чx3ЧT3Чs +1)
1) Влияние изменений моментов инерции тел.
a) Варьируем J3 (момент инерции ротора двигателя стабилизации):
Табл.12.
| J3 | T1 | T2 | T3 |
x2 |
x3 |
T4 |
x4 |
kw |
| 0.001 | 11.51 | 0.01145 | 0.000315 | 0.003737 | 0.015813 | 0.031623 | 0.000158 | 1.5 |
| 0.005 | 11.55 | 0.01159 | 0.000700 | 0.003691 | 0.006803 | 0.031623 | 0.000158 | 7.5 |
| 0.01 | 11.60 | 0.01175 | 0.000970 | 0.003634 | 0.004588 | 0.031623 | 0.000158 | 15 |
| 0.05 | 12.00 | 0.01295 | 0.001930 | 0.003206 | 0.001472 | 0.031623 | 0.000158 | 75 |
| 0.1 | 12.50 | 0.01426 | 0.002430 | 0.002766 | 0.000760 | 0.031623 | 0.000158 | 150 |
Характер изменения постоянных времени колебательных звеньев Т2, Т3, Т4 и коэффициента демпфирования в этих звеньях, представлен на графиках (Т3, d3 относятся к редуктору; T2, T4, d2, d4 - к креплению телекамеры):
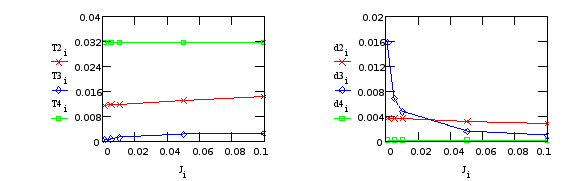
б) Варьируем J4 (момент инерции платформы):
Табл.13.
| J4 | T1 | T2 | T3 |
x2 |
x3 |
T4 |
x4 |
kw |
| 0.015 | 10.24990 | 0.004979 | 0.000768 | 0.011187 | 0.002402 | 0.031623 | 0.000158 | 1.5 |
| 0.075 | 10.84991 | 0.008857 | 0.000939 | 0.005476 | 0.004190 | 0.031623 | 0.000158 | 7.5 |
| 0.15 | 11.59992 | 0.011747 | 0.000968 | 0.003633 | 0.004588 | 0.031623 | 0.000158 | 15 |
| 0.75 | 17.59996 | 0.020780 | 0.000993 | 0.001021 | 0.004952 | 0.031623 | 0.000158 | 75 |
| 1.5 | 25.09997 | 0.024527 | 0.000997 | 0.000529 | 0.005001 | 0.031623 | 0.000158 | 150 |
Т3, d3 - от “редуктора”; T2, T4, d2, d4 - от крепления телекамеры.
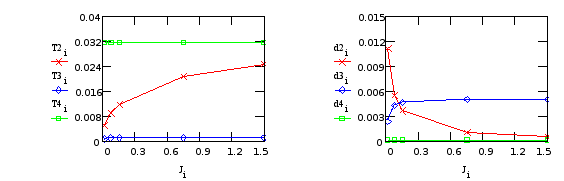
в) Варьируем J5 (момент инерции телекамеры):
Табл.14.
| J5 | T1 | T2 | T3 |
x2 |
x3 |
T4 |
x4 |
kw |
| 0.1 | 2.599976 | 0.007846 | 0.000968 | 0.001609 | 0.004588 | 0.01 | 0.0005 | 15.00000 |
| 0.5 | 6.599933 | 0.011012 | 0.000968 | 0.003102 | 0.004588 | 0.022361 | 0.000224 | 15.00000 |
| 1 | 11.59992 | 0.011747 | 0.000968 | 0.003634 | 0.004588 | 0.031623 | 0.000158 | 15.00000 |
| 5 | 51.59989 | 0.012454 | 0.000968 | 0.004219 | 0.004588 | 0.070711 | 0.000000 | 15.00000 |
| 10 | 101.5999 | 0.012552 | 0.000968 | 0.004305 | 0.004588 | 0.1 | 0.000000 | 14.99999 |
Т3, d3 - от “редуктора”; T2, T4, d2, d4 - от крепления телекамеры.
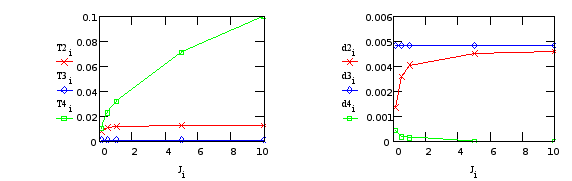
Из Табл.12...14 видно, что моменты инерции каждого из элементов модели сильно влияют только на одну из постоянных времени мало изменяя другие, поэтому в практических расчетах их можно считать независимыми.
2) Влияние нежесткостей редуктора С34 и крепления телекамеры к платформе С45.
а) Варьируем C34 (нежесткость редуктора):
Табл.15.
| C34 | T1 | T2 | T3 |
x2 |
x3 |
T4 |
x4 |
kw |
| 100 | 11.59894 | 0.012303 | 0.009243 | 0.020021 | 0.031623 | 0.031623 | 0.000158 | 15.00000 |
| 500 | 11.59973 | 0.011797 | 0.004311 | 0.004659 | 0.020062 | 0.031623 | 0.000158 | 15.00000 |
| 1000 | 11.59983 | 0.011769 | 0.003056 | 0.004070 | 0.014370 | 0.031623 | 0.000158 | 15.00000 |
| 5000 | 11.59991 | 0.011749 | 0.001367 | 0.003678 | 0.006482 | 0.031623 | 0.000158 | 15.00000 |
| 10000 | 11.59992 | 0.011747 | 0.000968 | 0.003634 | 0.004588 | 0.031623 | 0.000158 | 15.00000 |
| 50000 | 11.59992 | 0.011745 | 0.000433 | 0.003598 | 0.002053 | 0.031623 | 0.000158 | 15.00000 |
| 100000 | 11.59993 | 0.011745 | 0.000306 | 0.003594 | 0.001452 | 0.031623 | 0.000158 | 15.00000 |
Т3, d3 - от “редуктора”; T2, T4, d2, d4 - от крепления телекамеры.
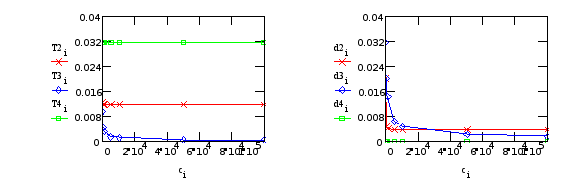
б) Варьируем C45 (нежесткость крепления телекамеры):
Табл.16.
| C45 | T1 | T2 | T3 |
x2 |
x3 |
T4 |
x4 |
kw |
| 100 | 11.59925 | 0.037141 | 0.000968 | 0.011366 | 0.004592 | 0.1 | 0.0005 | 15.00000 |
| 500 | 11.59984 | 0.016611 | 0.000968 | 0.005107 | 0.004590 | 0.044721 | 0.000224 | 15.00000 |
| 1000 | 11.59992 | 0.011747 | 0.000968 | 0.003634 | 0.004588 | 0.031623 | 0.000158 | 15.00000 |
| 5000 | 11.59998 | 0.005258 | 0.000967 | 0.001707 | 0.004569 | 0.014142 | 0.000071 | 15.00000 |
| 10000 | 11.59998 | 0.003722 | 0.000966 | 0.001287 | 0.004544 | 0.001 | 0.000050 | 15.00000 |
Т3, d3 - от “редуктора”; T2, T4, d2, d4 - от крепления телекамеры.
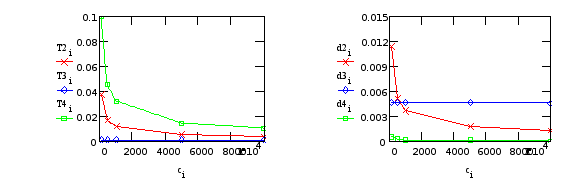
Из Табл.15,16 видно, что изменение нежесткости редуктора сильно меняет параметры только одного колебательного звена, появление которого вызвано нежесткостью редуктора, при этом параметры других звеньев практически не изменяются. Аналогично, нежесткость крепления телекамеры практически не влияет на колебательное звено появление которого вызывается нежесткостью редуктора. Это подтверждает вывод о том, что “колебательности” редуктора и крепления телекамеры можно рассматривать независимо.
3) Влияние демпфирования в редукторе D34 и элементах крепления телекамеры D45.
а) Варьируем D34 (редуктор):
Табл.17.
| D34 | T1 | T2 | T3 |
x2 |
x3 |
T4 |
x4 |
kw |
| 0.0001 | 11.59992 | 0.011747 | 0.000968 | 0.003624 | 0.004541 | 0.031623 | 0.000158 | 150 |
| 0.0005 | 11.59992 | 0.011747 | 0.000968 | 0.003624 | 0.004562 | 0.031623 | 0.000158 | 30 |
| 0.001 | 11.59992 | 0.011747 | 0.000968 | 0.003624 | 0.004588 | 0.031623 | 0.000158 | 15 |
| 0.005 | 11.59992 | 0.011747 | 0.000968 | 0.003624 | 0.004794 | 0.031623 | 0.000158 | 3 |
| 0.01 | 11.59992 | 0.011747 | 0.000968 | 0.003624 | 0.005053 | 0.031623 | 0.000158 | 1.5 |
Т3, d3 - от “редуктора”; T2, T4, d2, d4 - от крепления телекамеры.
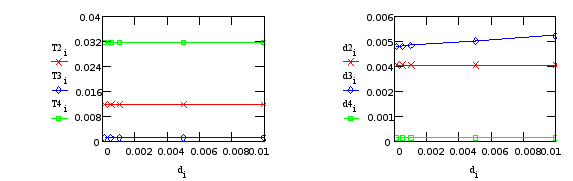
б) Варьируем D45 (крепление телекамеры):
Табл.18.
| D45 | T1 | T2 | T3 |
x2 |
x3 |
T4 |
x4 |
kw |
| 0.001 | 11.59992 | 0.011747 | 0.000968 | 0.003251 | 0.004586 | 0.031623 |
2.66Ч10-19 |
15.00000 |
| 0.005 | 11.59992 | 0.011747 | 0.000968 | 0.003421 | 0.004587 | 0.031623 | 0.000079 | 15.00000 |
| 0.01 | 11.59992 | 0.011747 | 0.000968 | 0.003634 | 0.004588 | 0.031623 | 0.000158 | 15.00000 |
| 0.05 | 11.59992 | 0.011747 | 0.000968 | 0.005335 | 0.004596 | 0.031623 | 0.000791 | 15.00000 |
| 0.1 | 11.59992 | 0.011747 | 0.000968 | 0.007463 | 0.004606 | 0.031623 | 0.001581 | 15.00000 |
Т3, d3 - от “редуктора”; T2, T4, d2, d4 - от крепления телекамеры.
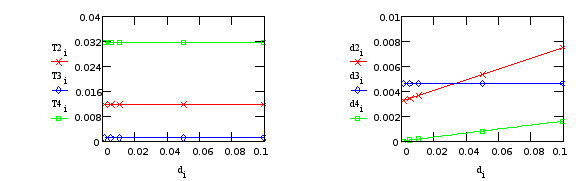
Из Табл.17,18 видно, что вариации коэффициента демпфирования в редукторе и креплении телекамеры не влияют на постоянные времени звеньев и, кроме того демпфирование в редукторе не влияет на коэффициенты демпфирования в колебательных звеньях, вызываемых нежестким креплением телекамеры, и, наоборот, изменение демпфирования в креплении телекамеры не влияет на коэффициент демпфирования в колебательном звене “от редуктора”.
Таким образом, можно сделать вывод, что в практических расчетах влияние нежесткостей редуктора и крепления телекамеры можно рассматривать независимо друг от друга.
Для частного случая, учитывающего только влияние нежесткости крепления объекта стабилизации к платформе на ЛАХ, возможно получение выражения для передаточной функции в символьном виде.
Для этого рассмотрим модель с “жестким” редуктором, т.е. полагая, что С34 бесконечно велико, и не учитывая нежесткость наружной рамы. Тогда базовая модель будет включать в себя только следующие элементы:
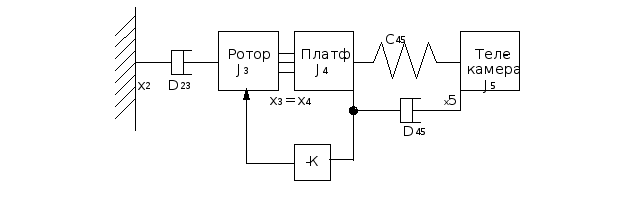
Рис.2.
J3 = 0.01 кгЧм2 - ротор;
J4 = 0.15 кгЧм2 -платформа;
J5 = 1 кгЧм2 - телекамера;
C45 =1Ч103 НЧм/рад. - нежесткость крепления телекамеры;
D23=0.1 НЧмЧс - демпфирование в двигателе стабилизации;
D45=0.01 НЧмЧс - демпфирование в креплении телекамеры;
К = 1000 - коэффициент передачи цепи обратной
связи.
В этом случае уравнения движения модели (1) с учетом того, что x3=x4 имеют следующий вид:
(J3+J4)Чx4''+D23Чx4'-D45Ч(x5'-x4')-C45Ч(x5-x4)=-KЧx4 (16)
J5Чx5''+D45Ч(x5'-x4')+C45Ч(x5-x4) = 0
Переписав в операторной форме и преобразовав, получим:
((J3+J4)Чs2+D23Чs +D45Чs+C45)Чx4-(D45Чs+C45)Чx5=-KЧx4 (17)
(J5Чs2+D45Чs+C45)Чx5-(D45Чs+C45)Чx4=0
Для нахождения передаточной функции разомкнутой системы по управляющему воздействию Wp(s) составим два определителя: главный - D, и характеризующий входное воздействие D1.
![]()
![]()
((J3+J4)Чs2+D23Чs +D45Чs+C45) -(D45Чs+C45)
D = (18)
-(D45Чs+C45) (J5Чs2+D45Чs+C45)
![]()
![]() -KЧx4 -(D45Чs+C45)
-KЧx4 -(D45Чs+C45)
D1 = (19)
0 (J5Чs2+D45Чs+C45)
Передаточная функция разомкнутой системы определяется как:
D1
![]() Wp(s)
= = (20)
Wp(s)
= = (20)
DЧx4
-KЧ(J5Чs2+D45Чs+C45)
![]() =
=
J5Ч(J3+J4)Чs4+(D23ЧJ5+D45Ч(J3+J4+J5))Чs3+(C45Ч(J3+J4+J5)+D23ЧD45)Чs2+C45ЧD23Чs
Пусть передаточная функция Wp(s) представляется в виде следующего выражения:
-KpЧ( T12 Ч s2 +2Чx1ЧT1Чs +1)
![]() Wp(s)= (21)
Wp(s)= (21)
s Ч (T3Чs+1)Ч( T22 Ч s2 +2Чx2ЧT2Чs +1)
Раскрывая скобки в (21), получаем:
-KpЧ( T12 Ч s2 +2Чx1ЧT1Чs +1)
![]() Wp(s)= (22)
Wp(s)= (22)
T22ЧT3Чs4+(T22+2Чx2ЧT2ЧT3)Чs3+(2Чx2ЧT2+T3)Чs2+s
Приравнивая члены при одинаковых степенях s в выражениях (20) и (22), получаем следующую систему уравнений:
T22ЧT3 = J5Ч(J3+J4)/(C45ЧD23)
T22+2Чx2ЧT2ЧT3 = (D23ЧJ5+D45Ч(J3+J4+J5))/(C45ЧD23) (23)
2Чx2ЧT2+T3 = ((J3+J4+J5)ЧC45+D23ЧD45)/(C45ЧD23)
Kp = K/D23
Решая систему уравнений (23), определим постоянные времени звеньев входящих в передаточную функцию Wp(s) (21):
J5
![]() T1
=
T1
=
C45
 J5Ч(J3+J4)
J5Ч(J3+J4)
![]() T2
= (24)
T2
= (24)
(J3+J4+J5)ЧC45+D23ЧD45
J3+J4+J5 D45
![]()
![]() T3
= Ч
T3
= Ч
D23
29-04-2015, 04:02
