Расчет постоянных времени передаточной функции проведенный по формулам (24) дает результат совпадающий с расчетом выполненныи с помощью численных методов.
Выводы сделаные ранее возможно представить в более общем виде. Модель приведенную на Рис.1 можно обобщить, представив ее в виде нескольких упруго-массовых элементов, соединенных последовательно и охваченных цепью обратной связи. Вид такой модели приведен на Рис.3.
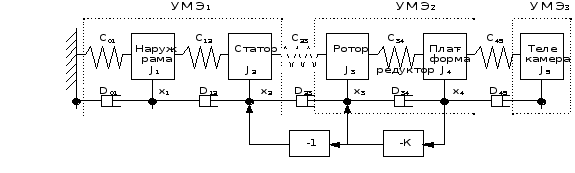
Рис. 3.
здесь УМЭ - упруго-массовый элемент.
Выводы:
1) Каждая колебательная система (Cij-Dij-Jj) в УМЭ1 (т.е. “слева” от контура стабилизации) приводит к появлению в передаточной функции разомкнутой системы Wp(s) пары из колебательного и антиколебательного звеньев имеющих одинаковые постоянные времени. Эти звенья взаимно компенсируют друг друга и, поэтому влияния на поведение ЛАХ практически не оказывют, однако из-за различия в коэффициентах демпфирования в этих звеньях, возникают выбросы на фазочастотной характеристике.
2) Колебательные системы в УМЭ2, (т.е. “внутри” контура стабилизации) вызывают появление в Wp(s) колебательных звеньев.
3) Колебательные системы в УМЭ3, т.е. находящиеся “за” чувствительным элементом, вызывают появление в Wp(s) пары из колебательного и антиколебательного звеньев постоянные времени которых, однако, не совпадают, причем антиколебательное звено всегда расположено на оси частот левее, чем колебательное, поэтому всегда имеет место местный “подъем” ЛАХ на +40 Дб/дек.
Программа построения ЛАХ непосредственным образом, без разложения на элементарные звенья.

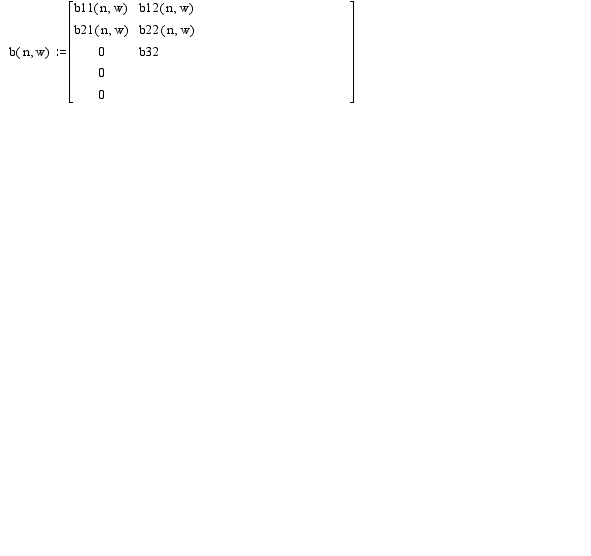
Программа определения корней полиномов числителя и знаменателя передаточной функции и построения ЛАХ по передаточной функции, состоящей из элементарных звеньев.
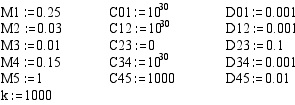
Вычисляю корни полиномов ai , b1 передаточной функции:
W(s) = (1/s)*(-K)*((b7*s7+b6*s6 + ... +b0)/(a9*s9 + a8*s8 + ... + a0))
Ввод 0,1,2....9
aa0:=........
aa1:=........
aa2:=........
aa3:=........
aa4:=........
aa5:=........
aa6:=........
aa7:=........
aa8:=........ (....... - выражения для aai, bbi см. записку)
aa9:=........
bb0:=........
bb1:=........
bb2:=........
bb3:=........
bb4:=........
bb5:=........
bb6:=........
bb7:=........

Определяю постоянные времени Тi (проверяй отрицательность действительной части).
Корни полиномов А и В следующие.
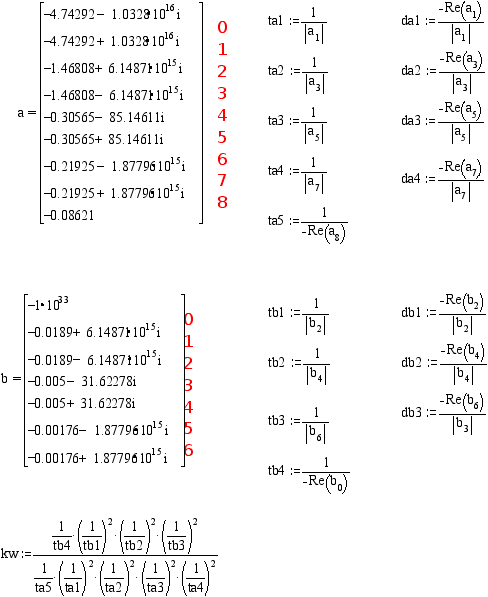
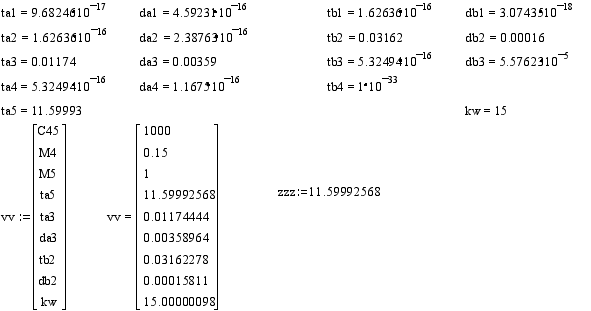
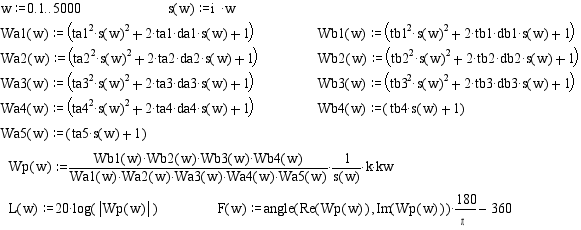
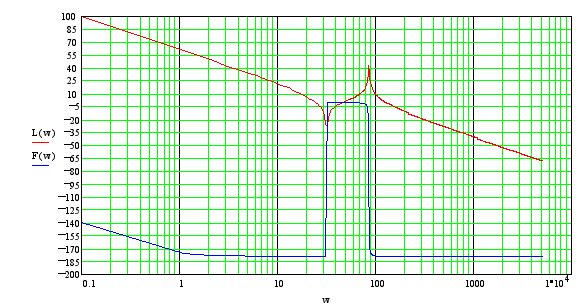
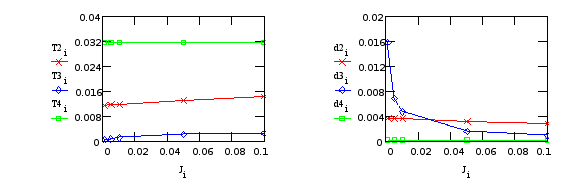
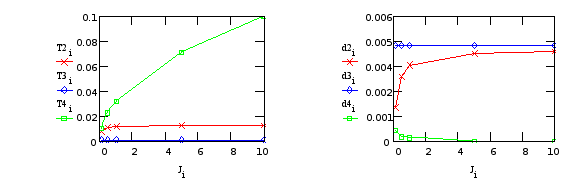
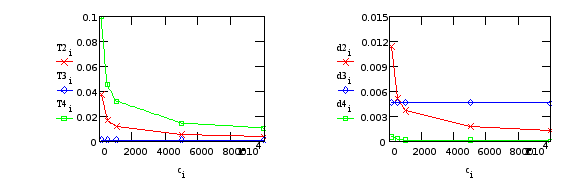
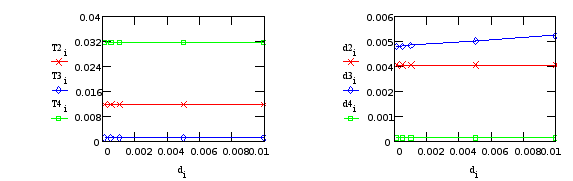
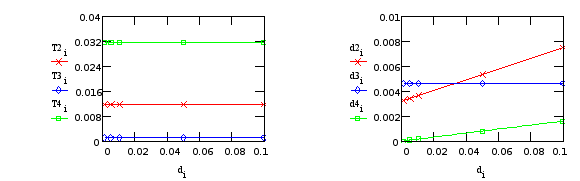
Программа вывода графических зависимостей для переменных входящих в состав передаточной функции.
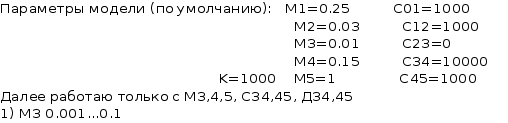


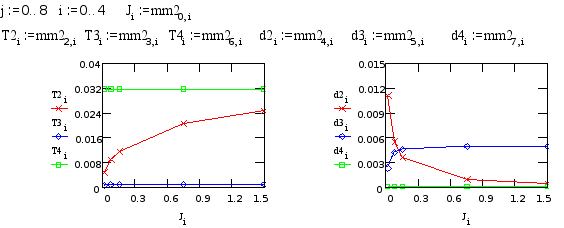
![]()

![]()
![]()
сс34:=

![]()
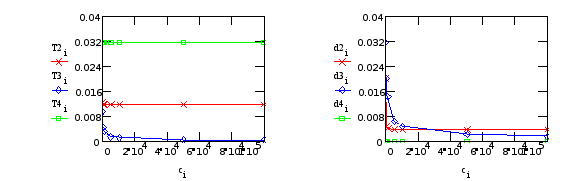
![]()

![]()
![]()

![]()
![]()

![]()
; Рабочая программа для пакета "DERIVE" для случая 1) - неподвижного основания.
; Входные данные.
; Условия неподвижности основания.
WX0:=0
WY0:=0
WZ0:=0
WX01:=0
WY01:=0
WZ01:=0
IYX1:=ixy1
IYX2:=ixy2
IZX1:=ixz1
IZX2:=ixz2
IZY1:=iyz1
IZY2:=iyz2
; Выражения для угловых скоростей.
WX1:=WX0 * COS(alfa) - WZ0 * SIN(alfa)
WY1:=WX1 * TAN(beta) + wy2 / COS(beta)
WZ1:=WX0 * SIN(alfa) + WZ0 * COS(alfa)
WX11:=WX01 * COS(alfa) - WZ01 * SIN(alfa)
WY11:=WX11 * TAN(beta) + wy21 / COS(beta)
WZ11:=WX01 * SIN(alfa) + WZ01 * COS(alfa)
WX2:=WX1 * COS(beta) + WY1 * SIN(beta)
WX21:=WX11 * COS(beta) + WY11 * SIN(beta)
; Выражения для моментов количества движения.
QX1:=ix1 * WX1 - ixy1 * WY1 - ixz1 * WZ1
QY1:=iy1 * WY1 - IYX1 * WX1 - iyz1 * WZ1
QZ1:=iz1 * WZ1 - IZX1 * WX1 - IZY1 * WY1
QX2:=ix2 * WX2 - ixy2 * wy2 - ixz2 * wz2
QY2:=iy2 * wy2 - IYX2 * WX2 - iyz2 * wz2
QZ2:=iz2 * wz2 - IZX2 * WX2 - IZY2 * wy2
QY11:=iy1 * WY11 - IYX1 * WX11 - iyz1 * WZ11
QX21:=ix2 * WX21 - ixy2 * wy21 - ixz2 * wz21
QY21:=iy2 * wy21 - IYX2 * WX21 - iyz2 * wz21
QZ21:=iz2 * wz21 - IZX2 * WX21 - IZY2 * wy21
; Выражения для возмущающих моментов.
MY1:=QY11 - QZ1 * WX1 + QX1 * WZ1
MX2:=QX21 - QY2 * wz2 + QZ2 * wy2
MY2:=QY21 - QZ2 * WX2 + QX2 * wz2
MZ2:=QZ21 - QX2 * wy2 + QY2 * WX2
MY1IN:=MY1 + MX2 * SIN(beta) + MY2 * COS(beta)
; Блок решения.
; Упрощение выражения для Mz2.
MZ2:= - ix2 * wy2^2 * TAN(beta) - ixz2 * wy21 * TAN(beta) + iy2 * wy2^2 * TAN(beta) - iyz2 * wy2 * wz2 * TAN(beta) - ixy2 * wy2^2 * TAN(beta)^2 + ixy2 * wy2^2 + ixz2 * wy2 * wz2 - iyz2 * wy21 + iz2 * wz21
; Упрощение выражения для My1.
MY1IN:= - ixy2 * wy2 * wz2 * COS(beta) - ixz2 * wz2^2 * COS(beta) + iy2 * wy21 * COS(beta) - iyz2 * wz21 * COS(beta) + ix2 * wy21 * SIN(beta)^2 / COS(beta) + ixy2 * wy2 * wz2 * SIN(beta)^2 / COS(beta) + iy1 * wy21 / COS(beta) + ix2 * wy2 * wz2 * SIN(beta) - 2 * ixy2 * wy21 * SIN(beta) - ixz2 * wz21 * SIN(beta) - iy2 * wy2 * wz2 * SIN(beta) + iyz2 * wz2^2 * SIN(beta)
; Рабочая программа для пакета "DERIVE" для случая 2) - неподвижной платформы.
; Входные данные.
; Условия неподвижности платформы.
WY2:=0
WY21:=0
WZ2:=0
WZ21:=0
IYX1:=ixy1
IYX2:=ixy2
IZX1:=ixz1
IZX2:=ixz2
IZY1:=iyz1
IZY2:=iyz2
; Выражения для угловых скоростей.
WX1:=wx0 * COS(alfa) - wz0 * SIN(alfa)
WY1:=WX1 * TAN(beta) + WY2 / COS(beta)
WZ1:=wx0 * SIN(alfa) + wz0 * COS(alfa)
WX11:=wx01 * COS(alfa) - wz01 * SIN(alfa)
WY11:=WX11 * TAN(beta) + WY21 / COS(beta)
WZ11:=wx01 * SIN(alfa) + wz01 * COS(alfa)
WX2:=WX1 * COS(beta) + WY1 * SIN(beta)
WX21:=WX11 * COS(beta) + WY11 * SIN(beta)
; Выражения для моментов количества движения.
QX1:=ix1 * WX1 - ixy1 * WY1 - ixz1 * WZ1
QY1:=iy1 * WY1 - IYX1 * WX1 - iyz1 * WZ1
QZ1:=iz1 * WZ1 - IZX1 * WX1 - IZY1 * WY1
QX2:=ix2 * WX2 - ixy2 * WY2 - ixz2 * WZ2
QY2:=iy2 * WY2 - IYX2 * WX2 - iyz2 * WZ2
QZ2:=iz2 * WZ2 - IZX2 * WX2 - IZY2 * WY2
QY11:=iy1 * WY11 - IYX1 * WX11 - iyz1 * WZ11
QX21:=ix2 * WX21 - ixy2 * WY21 - ixz2 * WZ21
QY21:=iy2 * WY21 - IYX2 * WX21 - iyz2 * WZ21
QZ21:=iz2 * WZ21 - IZX2 * WX21 - IZY2 * WY21
; Выражения для возмущающих моментов.
MY1:=QY11 - QZ1 * WX1 + QX1 * WZ1
MX2:=QX21 - QY2 * WZ2 + QZ2 * WY2
MY2:=QY21 - QZ2 * WX2 + QX2 * WZ2
MZ2:=QZ21 - QX2 * WY2 + QY2 * WX2
MY1IN:=MY1 + MX2 * SIN(beta) + MY2 * COS(beta)
; Блок решения.
; Упрощение выражения для Mz2.
MZ2:=ixy2 * wx0^2 * COS(beta)^2 * COS(alfa)^2 - ixy2 * wx0^2 * SIN(beta)^4 * COS(alfa)^2 / COS(beta)^2 - 2 * ixy2 * wx0^2 * COS(alfa)^2 - 2 * ixy2 * wx0 * wz0 * COS(beta)^2 * SIN(alfa) * COS(alfa) + 2 * ixy2 * wx0 * wz0 * SIN(beta)^4 * SIN(alfa) * COS(alfa) / COS(beta)^2 + 4 * ixy2 * wx0 * wz0 * SIN(alfa) * COS(alfa) - ixz2 * wx01 * COS(beta) * COS(alfa) - ixz2 * wx01 * SIN(beta)^2 * COS(alfa) / COS(beta) + ixy2 * wz0^2 * COS(beta)^2 * SIN(alfa)^2 - ixy2 * wz0^2 * SIN(beta)^4 * SIN(alfa)^2 / COS(beta)^2 - 2 * ixy2 * wz0^2 * SIN(alfa)^2 + ixz2 * wz01 * COS(beta) * SIN(alfa) + ixz2 * wz01 * SIN(beta)^2 * SIN(alfa) / COS(beta)
; Упрощение выражения для My1.
MY1IN:= - ixz2 * wx0^2 * COS(beta)^3 * COS(alfa)^2 + 2 * ixz2 * wx0^2 * COS(beta) * COS(alfa)^2 + ixz2 * wx0^2 * SIN(beta)^4 * COS(alfa)^2 / COS(beta) - ixy1 * wx0 * wz0 * TAN(beta) * COS(alfa)^2 + iyz1 * wx0^2 * TAN(beta) * COS(alfa)^2 + ix1 * wx0 * wz0 * COS(alfa)^2 + ixz1 * wx0^2 * COS(alfa)^2 - ixz1 * wz0^2 * COS(alfa)^2 - iz1 * wx0 * wz0 * COS(alfa)^2 + 2 * ixz2 * wx0 * wz0 * COS(beta)^3 * SIN(alfa) * COS(alfa) - 4 * ixz2 * wx0 * wz0 * COS(beta) * SIN(alfa) * COS(alfa) - 2 * ixz2 * wx0 * wz0 * SIN(beta)^4 * SIN(alfa) * COS(alfa) / COS(beta) - ixy1 * wx0^2 * TAN(beta) * SIN(alfa) * COS(alfa) + ixy1 * wz0^2 * TAN(beta) * SIN(alfa) * COS(alfa) - 2 * iyz1 * wx0 * wz0 * TAN(beta) * SIN(alfa) * COS(alfa) + ix1 * wx0^2 * SIN(alfa) * COS(alfa) - ix1 * wz0^2 * SIN(alfa) * COS(alfa) - 4 * ixz1 * wx0 * wz0 * SIN(alfa) * COS(alfa) - iz1 * wx0^2 * SIN(alfa) * COS(alfa) + iz1 * wz0^2 * SIN(alfa) * COS(alfa) + ix2 * wx01 * SIN(beta) * COS(beta) * COS(alfa) + ix2 * wx01 * SIN(beta)^3 * COS(alfa) / COS(beta) + iy1 * wx01 * TAN(beta) * COS(alfa) - ixy1 * wx01 * COS(alfa) - ixy2 * wx01 * COS(alfa) - iyz1 * wz01 * COS(alfa) - ixz2 * wz0^2 * COS(beta)^3 * SIN(alfa)^2 + 2 * ixz2 * wz0^2 * COS(beta) * SIN(alfa)^2 + ixz2 * wz0^2 * SIN(beta)^4 * SIN(alfa)^2 / COS(beta) + ixy1 * wx0 * wz0 * TAN(beta) * SIN(alfa)^2 + iyz1 * wz0^2 * TAN(beta) * SIN(alfa)^2 - ix1 * wx0 * wz0 * SIN(alfa)^2 - ixz1 * wx0^2 * SIN(alfa)^2 + ixz1 * wz0^2 * SIN(alfa)^2 + iz1 * wx0 * wz0 * SIN(alfa)^2 - ix2 * wz01 * SIN(beta) * COS(beta) * SIN(alfa) - ix2 * wz01 * SIN(beta)^3 * SIN(alfa) / COS(beta) - iy1 * wz01 * TAN(beta) * SIN(alfa) + ixy1 * wz01 * SIN(alfa) + ixy2 * wz01 * SIN(alfa) - iyz1 * wx01 * SIN(alfa)
Рабочая программа для пакета "DERIVE" с проведенными предварительными вычислениями.
; Входные данные.
; Переприсвоение моментов инерции.
IYX1:=ixy1
IYX2:=ixy2
IZX1:=ixz1
IZX2:=ixz2
IZY1:=iyz1
IZY2:=iyz2
; Выражения для угловых скоростей.
WX1:=wx0 * COS(alfa) - wz0 * SIN(alfa)
WY1:=WX1 * TAN(beta) + wy2 / COS(beta)
WZ1:=wx0 * SIN(alfa) + wz0 * COS(alfa)
WX11:=wx01 * COS(alfa) - wz01 * SIN(alfa)
WY11:=WX11 * TAN(beta) + wy21 / COS(beta)
WZ11:=wx01 * SIN(alfa) + wz01 * COS(alfa)
WX2:=WX1 * COS(beta) + WY1 * SIN(beta)
WX21:=WX11 * COS(beta) + WY11 * SIN(beta)
; Выражения для моментов количества движения.
QX1:=ix1 * WX1 - ixy1 * WY1 - ixz1 * WZ1
QY1:=iy1 * WY1 - IYX1 * WX1 - iyz1 * WZ1
QZ1:=iz1 * WZ1 - IZX1 * WX1 - IZY1 * WY1
QX2:=ix2 * WX2 - ixy2 * wy2 - ixz2 * wz2
QY2:=iy2 * wy2 - IYX2 * WX2 - iyz2 * wz2
QZ2:=iz2 * wz2 - IZX2 * WX2 - IZY2 * wy2
QY11:=iy1 * WY11 - IYX1 * WX11 - iyz1 * WZ11
QX21:=ix2 * WX21 - ixy2 * wy21 - ixz2 * wz21
QY21:=iy2 * wy21 - IYX2 * WX21 - iyz2 * wz21
QZ21:=iz2 * wz21 - IZX2 * WX21 - IZY2 * wy21
; Выражения для возмущающих моментов.
MY1:=QY11 - QZ1 * WX1 + QX1 * WZ1
MX2:=QX21 - QY2 * wz2 + QZ2 * wy2
MY2:=QY21 - QZ2 * WX2 + QX2 * wz2
MZ2:=QZ21 - QX2 * wy2 + QY2 * WX2
MY1IN:=MY1 + MX2 * SIN(beta) + MY2 * COS(beta)
; Блок решения.
; Раскрытие выражения для Mz2 по всем переменным.
MZ2:=ixy2 * wx0^2 * COS(beta)^2 * COS(alfa)^2 - ixy2 * wx0^2 * SIN(beta)^4 * COS(alfa)^2 / COS(beta)^2 - 2 * ixy2 * wx0^2 * COS(alfa)^2 - 2 * ixy2 * wx0 * wz0 * COS(beta)^2 * SIN(alfa) * COS(alfa) + 2 * ixy2 * wx0 * wz0 * SIN(beta)^4 * SIN(alfa) * COS(alfa) / COS(beta)^2 + 4 * ixy2 * wx0 * wz0 * SIN(alfa) * COS(alfa) - ix2 * wx0 * wy2 * COS(beta) * COS(alfa) - ixz2 * wx01 * COS(beta) * COS(alfa) + iy2 * wx0 * wy2 * COS(beta) * COS(alfa) - iyz2 * wx0 * wz2 * COS(beta) * COS(alfa) - ix2 * wx0 * wy2 * SIN(beta)^2 * COS(alfa) / COS(beta) - ixz2 * wx01 * SIN(beta)^2 * COS(alfa) / COS(beta) + iy2 * wx0 * wy2 * SIN(beta)^2 * COS(alfa) / COS(beta) - iyz2 * wx0 * wz2 * SIN(beta)^2 * COS(alfa) / COS(beta) - 2 * ixy2 * wx0 * wy2 * SIN(beta)^3 * COS(alfa) / COS(beta)^2 - 2 * ixy2 * wx0 * wy2 * SIN(beta) * COS(alfa) + ixy2 * wz0^2 * COS(beta)^2 * SIN(alfa)^2 - ixy2 * wz0^2 * SIN(beta)^4 * SIN(alfa)^2 / COS(beta)^2 - 2 * ixy2 * wz0^2 * SIN(alfa)^2 + ix2 * wy2 * wz0 * COS(beta) * SIN(alfa) + ixz2 * wz01 * COS(beta) * SIN(alfa) - iy2 * wy2 * wz0 * COS(beta) * SIN(alfa) + iyz2 * wz0 * wz2 * COS(beta) * SIN(alfa) + ix2 * wy2 * wz0 * SIN(beta)^2 * SIN(alfa) / COS(beta) + ixz2 * wz01 * SIN(beta)^2 * SIN(alfa) / COS(beta) - iy2 * wy2 * wz0 * SIN(beta)^2 * SIN(alfa) / COS(beta) + iyz2 * wz0 * wz2 * SIN(beta)^2 * SIN(alfa) / COS(beta) + 2 * ixy2 * wy2 * wz0 * SIN(beta)^3 * SIN(alfa) / COS(beta)^2 + 2 * ixy2 * wy2 * wz0 * SIN(beta) * SIN(alfa) - ix2 * wy2^2 * TAN(beta) - ixz2 * wy21 * TAN(beta) + iy2 * wy2^2 * TAN(beta) - iyz2 * wy2 * wz2 * TAN(beta) - ixy2 * wy2^2 * TAN(beta)^2 + ixy2 * wy2^2 + ixz2 * wy2 * wz2 - iyz2 * wy21 + iz2 * wz21
; Раскрытие скобок по всем переменным в выражении
; для My1.
MY1IN:= - ixz2 * wx0^2 * COS(beta)^3 * COS(alfa)^2 + 2 * ixz2 * wx0^2 * COS(beta) * COS(alfa)^2 + ixz2 * wx0^2 * SIN(beta)^4 * COS(alfa)^2 / COS(beta) - ixy1 * wx0 * wz0 * TAN(beta) * COS(alfa)^2 + iyz1 * wx0^2 * TAN(beta) * COS(alfa)^2 + ix1 * wx0 * wz0 * COS(alfa)^2 + ixz1 * wx0^2 * COS(alfa)^2 - ixz1 * wz0^2 * COS(alfa)^2 - iz1 * wx0 * wz0 * COS(alfa)^2 + 2 * ixz2 * wx0 * wz0 * COS(beta)^3 * SIN(alfa) * COS(alfa) - 4 * ixz2 * wx0 * wz0 * COS(beta) * SIN(alfa) * COS(alfa) - 2 * ixz2 * wx0 * wz0 * SIN(beta)^4 * SIN(alfa) * COS(alfa) / COS(beta) - ixy1 * wx0^2 * TAN(beta) * SIN(alfa) * COS(alfa) + ixy1 * wz0^2 * TAN(beta) * SIN(alfa) * COS(alfa) - 2 * iyz1 * wx0 * wz0 * TAN(beta) * SIN(alfa) * COS(alfa) + ix1 * wx0^2 * SIN(alfa) * COS(alfa) - ix1 * wz0^2 * SIN(alfa) * COS(alfa) - 4 * ixz1 * wx0 * wz0 * SIN(alfa) * COS(alfa) - iz1 * wx0^2 * SIN(alfa) * COS(alfa) + iz1 * wz0^2 * SIN(alfa) * COS(alfa) + ix2 * wx01 * SIN(beta) * COS(beta) * COS(alfa) + ixy2 * wx0 * wz2 * SIN(beta) * COS(beta) * COS(alfa) + ixz2 * wx0 * wy2 * SIN(beta) * COS(beta) * COS(alfa) + ix2 * wx01 * SIN(beta)^3 * COS(alfa) / COS(beta) + ixy2 * wx0 * wz2 * SIN(beta)^3 * COS(alfa) / COS(beta) + ixz2 * wx0 * wy2 * SIN(beta)^3 * COS(alfa) / COS(beta) + iy1 * wx01 * TAN(beta) * COS(alfa) - ixy1 * wy2 * wz0 * COS(alfa) / COS(beta) + iyz1 * wx0 * wy2 * COS(alfa) / COS(beta) + ix2 * wx0 * wz2 * COS(alfa) - ixy1 * wx01 * COS(alfa) - ixy2 * wx01 * COS(alfa) - iyz1 * wz01 * COS(alfa) + iyz2 * wx0 * wy2 * COS(alfa) - iz2 * wx0 * wz2 * COS(alfa) - ixz2 * wz0^2 * COS(beta)^3 * SIN(alfa)^2 + 2 * ixz2 * wz0^2 * COS(beta) * SIN(alfa)^2 + ixz2 * wz0^2 * SIN(beta)^4 * SIN(alfa)^2 / COS(beta) + ixy1 * wx0 * wz0 * TAN(beta) * SIN(alfa)^2 + iyz1 * wz0^2 * TAN(beta) * SIN(alfa)^2 - ix1 * wx0 * wz0 * SIN(alfa)^2 - ixz1 * wx0^2 * SIN(alfa)^2 + ixz1 * wz0^2 * SIN(alfa)^2 + iz1 * wx0 * wz0 * SIN(alfa)^2 - ix2 * wz01 * SIN(beta) * COS(beta) * SIN(alfa) - ixy2 * wz0 * wz2 * SIN(beta) * COS(beta) * SIN(alfa) - ixz2 * wy2 * wz0 * SIN(beta) * COS(beta) * SIN(alfa) - ix2 * wz01 * SIN(beta)^3 * SIN(alfa) / COS(beta) - ixy2 * wz0 * wz2 * SIN(beta)^3 * SIN(alfa) / COS(beta) - ixz2 * wy2 * wz0 * SIN(beta)^3 * SIN(alfa) / COS(beta) - iy1 * wz01 * TAN(beta) * SIN(alfa) - ixy1 * wx0 * wy2 * SIN(alfa) / COS(beta) - iyz1 * wy2 * wz0 * SIN(alfa) / COS(beta) - ix2 * wz0 * wz2 * SIN(alfa) + ixy1 * wz01 * SIN(alfa) + ixy2 * wz01 * SIN(alfa) - iyz1 * wx01 * SIN(alfa) - iyz2 * wy2 * wz0 * SIN(alfa) + iz2 * wz0 * wz2 * SIN(alfa) - ixy2 * wy2 * wz2 * COS(beta) - ixz2 * wz2^2 * COS(beta) + iy2 * wy21 * COS(beta) - iyz2 * wz21 * COS(beta) + ix2 * wy21 * SIN(beta)^2 / COS(beta) + ixy2 * wy2 * wz2 * SIN(beta)^2 / COS(beta) + iy1 * wy21 / COS(beta) + ix2 * wy2 * wz2 * SIN(beta) - 2 * ixy2 * wy21 * SIN(beta) - ixz2 * wz21 * SIN(beta) - iy2 * wy2 * wz2 * SIN(beta) + iyz2 * wz2^2 * SIN(beta)
Рабочая программа для пакета “DERIVE” определения коэффициентов при степенях s в полиноме знаменателя передаточной функции разомкнутой системы Wp(s).
; Входные данные.
; Определитель исходной матрицы.
DET([[m1 * s^2 + d01 * s + d12 * s + c01 + c12,- d12 * s - c12,0,0,0],
[ - d12 * s - c12, m2 * s^2 + d12 * s + d23 * s + c12, - d23 * s, 0, 0],
[0, - d23 * s, m3 * s^2 + (d23 + d34) * s + c34, - (d34 * s + c34), 0],
[0, 0, - (d34 * s + c34), m4 * s^2 + (d34 + d45) * s + (c34 + c45), - (d45 * s + c45)],
[0, 0, 0, - (d45 * s + c45), m5 * s^2 + d45 * s + c45]])
; Блок решения.
; Результат нахождения определителя.
m1 * m2
29-04-2015, 04:02
