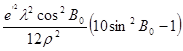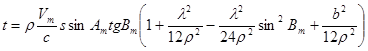b
6356863,019
e2
0,00669342
ρº
57,29577951
Результати вимірів кутів
| № трикутника |
Позначення кутів |
Виміряні сферичні кути |
| 1 |
A1 |
78º27′09.18" |
| B1 |
51º33′02.51" |
|
| C1 |
49º59′51.20" |
|
| 2 |
A2 |
59º25′19.10" |
| B2 |
51º46′48.52" |
|
| C2 |
68º47′54.33" |
Робочі формули:
![]()
Трикутник №1:
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Трикутник №2:
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Відомість наближеного розв’язування трикутників
| Верш. |
Виміряні сферичні кути |
|
Виправлені сферичні кути |
Синуси кутів |
Приблизні довжини |
Аддита- менти |
Довжини сторін |
| C |
49º59′51.20" |
1,689 |
49º59′52.888" |
0,76601402 |
- |
0,00001284 |
56000,000 |
| B |
51º33′02.51" |
1,689 |
51º33′04.198" |
0,78315577 |
57253,127 |
0,00001342 |
57253,160 |
| A |
78º27′09.18" |
1,689 |
78º27′10.868" |
0,97975833 |
71625,345 |
0,00002100 |
71625,930 |
| Σ1 |
180º00′02.89" |
5,066 |
180º00′07.956" |
||||
| ε1 |
7,956 |
||||||
| w1 |
-5,066 |
||||||
| D |
59º25′19.10" |
3,035 |
59º25′22.134" |
0,86093557 |
- |
0,00002100 |
71625,930 |
| B |
51º46′48.52" |
3,035 |
51º46′51.554" |
0,78564059 |
65361,959 |
0,00001749 |
65361,729 |
| C |
68º47′54.33" |
3,035 |
68º47′57.364" |
0,93231272 |
77563,903 |
0,00002462 |
77564,185 |
| Σ2 |
180º00′01.95" |
9,105 |
180º00′11.052" |
||||
| ε2 |
11,055 |
||||||
| w2 |
-9,105 |
Завдання 6. Розв’язування прямої геодезичної задачі способом допоміжної точки (спосіб Шрейбера)
Розв’язування прямої геодезичної задачі способом допоміжної точки виконується посереднім шляхом – обраховують насамперед різниці координат пунктів, а за ними – абсолютні значення координат. За умови використання робочих формул приведеного нижче вигляду, спосіб забезпечує розрахунок геодезичних координат пунктів у тріангуляції 1 класу з точністю десятитисячних часток секунди, азимутів – з точністю тисячних часток секунди.
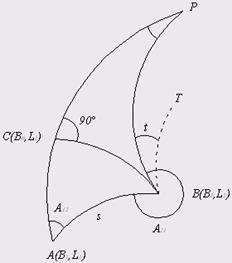
A і В – пункти на поверхні еліпсоїду з геодезичними координатами B1 ,L1 і B2 ,L2 . АР – меридіан т.А; ВР – меридіан т.В. А12 і А21 – прямий і зворотній азимут напряму АВ. s – довжина геодезичної лінії АВ. С – допоміжна точка поверхні еліпсоїду, розташована на меридіані т.A так, що геодезична лінія СВ має азимут АСВ = 90º. Точка С має геодезичні координати B0 , L1 .
Черговість дій при розв’язуванні прямої геодезичної задачі способом допоміжної точки:
1. Обчислення широти точки С
![]() - перша функція геодезичної широти пункту А;
- перша функція геодезичної широти пункту А;
![]() - радіус кривизни меридіанного перерізу в п. А;
- радіус кривизни меридіанного перерізу в п. А;
![]() ;
; ![]() - проміжні умовні позначення; b – різниця широт п.А і т.С.
- проміжні умовні позначення; b – різниця широт п.А і т.С.
2. Обчислення широти пункту В
![]()
![]()
![]()
![]()
![]()
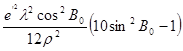 ,
,
d – різниця широт п.В і т.С,
![]()
![]()
![]() ,
,
с – різниця довгот пункту В і точки С,
![]() ,
, ![]()
![]() - проміжні величини.
- проміжні величини.
3. Обчислення довготи пункту В
λ = ![]()
![]() ,
,
λ - різниця довгот пунктів А і В,
4. Обчислення зворотного азимуту А21
А21
= ![]() , t – кут, утворений на поверхні еліпсоїду кривою ВР меридіанного перерізу в пункті В та кривою ВТ, яка паралельна меридіанному перерізові у пункті А, ε - сферичний надлишок трикутника АВС.
, t – кут, утворений на поверхні еліпсоїду кривою ВР меридіанного перерізу в пункті В та кривою ВТ, яка паралельна меридіанному перерізові у пункті А, ε - сферичний надлишок трикутника АВС.
Вихідні дані
Номер варіанту №8
| B1 = 48º01′01.1111"+7′*8 |
48º57′01.1111" |
48,95030864 |
| L1 = 22º11′11.1111"+30′*8 |
26º11′11.1111" |
26,18641975 |
| A12 = 1º01′01.111"+3º*8 |
25º01′01.111" |
25,01697528 |
| s = (60000 – 500*8) |
56000 м |
Сталі величини
| a |
6378245 м |
e2 |
0,00669342 |
e’2 |
0,00673853 |
ρº |
57,29577951 |
Обчислення широти точки С
| Позначення дій |
Результати |
Позначення дій |
Результати |
|
|
0,998094819 |
|
0,456307116 |
|
|
6371902,273 |
|
0,00003975 |
|
|
50746,22203 |
|
0,00000459 |
|
|
23681,65851 |
|
-0,00000003 |
| b |
0,456291085 |
B0 |
49,40659972 |
| 0º27′22.65" |
49º24′23.76" |
Обчислення широти пункту В
| Позначення дій |
Результати |
Позначення дій |
Результати |
|
|
0,99806840 |
|
0,00046040 |
|
|
0,21232144 |
|
0,00000312 |
|
|
0,00001054 |
|
0,00000270 |
| с |
0,21231920 |
|
0,00000004 |
|
|
0,32630018 |
d |
0,00046039 |
|
|
0,24777482 |
B2 |
49,40613933 |
| 49º24′22.1" |
Обчислення довготи пункту В
| Позначення дій |
Результати |
Позначення дій |
Результати |
|
|
0,00000623 |
λ |
0,32629814 |
|
|
0,00000000 |
L2 |
26,51271789 |
| 26º30′45.78" |
Обчислення зворотного азимуту
| Позначення дій |
Результати |
Позначення дій |
Результати |
|
|
0,00084549 |
t |
0,247772701 |
|
|
0,00000541 |
A21 |
205,26390249 |
|
|
0,00000003 |
205º15′50" |
Завдання 7. Розв’язування прямої геодезичної задачі за формулами Гауса із середніми аргументами
Вихідні дані та сталі величини наведено у завданні №6.
| Наближення (1) |
||||
| Позначення дій |
Результати |
Позначення дій |
Результати |
|
|
|
6399698,916 |
|
1,001452017 |
|
|
|
0,456307116 |
|
0,243826934 |
|
|
|
0,32331773 |
|||
|
|
49,1784622 |
|
25,13888874 |
|
| Позначення дій |
Результати в наближеннях |
|||
| (2) |
(3) |
(4) |
(5) |
|
|
|
1,00143875 |
1,00143875 |
1,001438754 |
1,001438754 |
|
|
0,000002654 |
0,000002702 |
0,000002703 |
0,000002703 |
|
|
0,000000760 |
0,000000774 |
0,000000774 |
0,000000774 |
|
|
0,00000264 |
0,00000264 |
0,00000264 |
0,00000264 |
|
|
0,45583487 |
0,45582911 |
0,45582908 |
0,45582908 |
|
|
0,32628147 |
0,32629866 |
0,32629871 |
0,32629871 |
|
|
0,24691330 |
0,24692543 |
0,24692546 |
0,24692546 |
| b |
0,455836428 |
0,45583069 |
0,45583067 |
0,45583067 |
| λ |
0,326280859 |
0,32629805 |
0,32629811 |
0,32629811 |
| t |
0,24691507 |
0,24692721 |
0,24692724 |
0,24692724 |
|
|
49,17822685 |
49,17822398 |
49,17822397 |
49,17822397 |
|
|
25,14043282 |
25,14043888 |
25,14043890 |
25,14043890 |
Кінцеві результати
| Позначення дій |
Результати |
|
|
|
49,40613931 |
49º24′22.1" |
|
|
26,51271786 |
26º30′45.78" |
|
|
205,26390252 |
205º15′50" |
Завдання 8. Розв’язування оберненої геодезичної задачі за формулами Гауса із середніми аргументами
Для розв’язування оберненої геодезичної задачі, в якій за значенням геодезичних координат B1 , L1 та B2 , L2 пунктів А та В розраховують значення азимутів А12 , А21 та довжини s геодезичної лінії АВ, найбільш оптимально використовувати обернений алгоритм розв’язування за формулами Гауса із середніми аргументами.
У порівнянні з іншими способами розв’язування оберненої геодезичної задачі спосіб Гауса із середніми аргументами виділяється простотою робочих формул, тому розглядається як найбільш оптимальний.
Черговість дій при розв’язуванні оберненої геодезичної задачі за формулами Гауса із середніми аргументами:
1. Обчислення різниць координат ![]() ,
, ![]() та середньої широти
та середньої широти ![]() .
.
2. Обчислення середнього азимуту Аm
![]() ,
,
за знаками P та Q визначають четверть, в якій розташований напрям Аm .
3. Обчислення довжини геодезичної лінії
![]() або
або ![]() .
.
4. Обчислення зближення меридіанів t
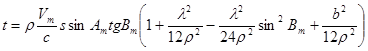 .
.
5. Обчислення азимутів
![]() та
та ![]() .
.
Наведені формули за точністю результатів розрахунків дійсні для віддалей такого ж порядку, що й у прямій геодезичній задачі.
Вихідні дані
Номер варіанту №8
| B1 = 48º01′01.1111"+7′*8 |
48º57′01.1111" |
48,95030864 |
| L1 = 22º11′11.1111"+30′*8 |
26º11′11.1111" |
26,18641975 |
| B2 |
49º24′22.1" |
49,40613931 |
| L2 |
26º30′45.78" |
26,51271786 |
Геодезичні координати пункту В вибрано із завдання №7.
Сталі величини
| a |
6378245 м |
e’2 |
0,00673853 |
ρº |
57,29577951 |
| Позначення дій |
Результати |
Позначення дій |
Результати |
| 1. Обчислення різниць координат і середньої широти |
|||
|
|
0,45583067 |
|
49,17822397 |
|
|
0,32629811 |
||
| 2. Обчислення сумм поправочних коефіцієнтів |
|||
|
|
0,00000270 |
Δb |
1,00000348 |
|
|
0,00000264 |
||
|
|
0,00000077 |
Δλ |
0,99999814 |
| 3. Обчислення середнього азимуту Аm |
|||
|
|
6399698,916 |
|
23790,954 |
|
|
1,001438768 |
|
25,14043968 |
|
|
50695,072 |
|
25º8′25.58" |
| 4. Обчислення довжини геодезичної лінії s |
|||
|
|
55999,998 м |
|
55999,998 м |
| 5. Обчислення зближення меридіанів t |
|||
|
|
0,24692546 |
|
1,00000720 |
|
|
0,24692724 |
||
| 6. Обчислення азимутів |
|||
|
|
25,01697606 |
|
205,26390330 |
| 25º1′1.11" |
205º15′50" |
||
Завдання 9. Пряма задача проекції Гауса-Крюгера (перехід з поверхні еліпсоїду на площину)
Прямою задачею Гауса – Крюгера називають розв’язування завдання переходу з поверхні еліпсоїду на площину з метою визначення прямокутних координат пунктів, якщо вихідними даними є геодезичні координати B, L початкового пункту А, довжина геодезичної лінії s та азимуту ААВ вихідної сторони АВ мережі геодезичних пунктів.
29-04-2015, 00:38