(3;3): -3 + 13 > 5; ∆33 = -3 + 13 - 5 = 5
max(7,12,13,5) = 13
Вибираємо максимальну оцінку вільної клітини (2;2): 5
Для цього в перспективну клітку (2;2) поставимо знак «+», а в інших вершинах багатокутника чергуються знаки «-», «+», «-».
| Завод №1 |
Завод №2 |
Завод №3 |
Завод №4 |
Завод №5 |
Запаси |
|
| Ферма №1 |
20[11] |
16[9][-] |
13[5][+] |
15 |
11 |
25 |
| Ферма №2 |
10 |
5[+] |
15[3][-] |
10[2] |
23 |
5 |
| Ферма №3 |
25 |
20 |
5 |
5[4] |
15[6] |
10 |
| Потреби |
11 |
9 |
8 |
6 |
6 |
Цикл наведено в таблиці (2,2; 2,3; 1,3; 1,2; ).
З вантажів хij стоять у мінусових клітинах, вибираємо найменше, тобто у = min (2, 3) = 3. Додаємо 3 до обсягів вантажів, що стоять у плюсових клітинах і віднімаємо 3 з Хij, стоять у мінусових клітинах. У результаті отримаємо новий опорний план.
| Завод №1 |
Завод №2 |
Завод №3 |
Завод №4 |
Завод №5 |
Запаси |
|
| Ферма №1 |
20[11] |
16[6] |
13[8] |
15 |
11 |
25 |
| Ферма №2 |
10 |
5[3] |
15 |
10[2] |
23 |
5 |
| Ферма №3 |
25 |
20 |
5 |
5[4] |
15[6] |
10 |
| Потреби |
11 |
9 |
8 |
6 |
6 |
Перевіримо оптимальність опорного плану. Знайдемо попередні потенціали ui, vi. по зайнятих клітинам таблиці, в яких ui + vi = cij, вважаючи, що u1 = 0.
u1 + v1 = 20; 0 + v1 = 20; v1 = 20
u1 + v2 = 16; 0 + v2 = 16; v2 = 16
u2 + v2 = 5; 16 + u2 = 5; u2 = -11
u2 + v4 = 10; -11 + v4 = 10; v4 = 21
u3 + v4 = 5; 21 + u3 = 5; u3 = -16
u3 + v5 = 15; -16 + v5 = 15; v5 = 31
u1 + v3 = 13; 0 + v3 = 13; v3 = 13
| v1 =20 |
v2 =16 |
v3 =13 |
v4 =21 |
v5 =31 |
|
| u1 =0 |
20[11] |
16[6] |
13[8] |
15 |
11 |
| u2 =-11 |
10 |
5[3] |
15 |
10[2] |
23 |
| u3 =-16 |
25 |
20 |
5 |
5[4] |
15[6] |
Опорний план не є оптимальним, тому що існують оцінки вільних клітин, для яких ui + vi > cij
(1;4): 0 + 21 > 15; ∆14 = 0 + 21 - 15 = 6
(1;5): 0 + 31 > 11; ∆15 = 0 + 31 - 11 = 20
max(6,20) = 20
Вибираємо максимальну оцінку вільної клітини (1;5): 11
Для цього в перспективну клітку (1;5) поставимо знак «+», а в інших вершинах багатокутника чергуються знаки «-», «+», «-».
| Завод №1 |
Завод №2 |
Завод №3 |
Завод №4 |
Завод №5 |
Запаси |
|
| Ферма №1 |
20[11] |
16[6][-] |
13[8] |
15 |
11[+] |
25 |
| Ферма №2 |
10 |
5[3][+] |
15 |
10[2][-] |
23 |
5 |
| Ферма №3 |
25 |
20 |
5 |
5[4][+] |
15[6][-] |
10 |
| Потреби |
11 |
9 |
8 |
6 |
6 |
Цикл наведено в таблиці (1,5; 1,2; 2,2; 2,4; 3,4; 3,5; ).
З вантажів хij стоять у мінусових клітинах, вибираємо найменше, тобто у = min (2, 4) = 2. Додаємо 2 до обсягів вантажів, що стоять у плюсових клітинах і віднімаємо 2 з Хij, стоять у мінусових клітинах. У результаті отримаємо новий опорний план.
| Завод №1 |
Завод №2 |
Завод №3 |
Завод №4 |
Завод №5 |
Запаси |
|
| Ферма №1 |
20[11] |
16[4] |
13[8] |
15 |
11[2] |
25 |
| Ферма №2 |
10 |
5[5] |
15 |
10 |
23 |
5 |
| Ферма №3 |
25 |
20 |
5 |
5[6] |
15[4] |
10 |
| Потреби |
11 |
9 |
8 |
6 |
6 |
Перевіримо оптимальність опорного плану. Знайдемо попередні потенціали ui, vi. по зайнятих клітинам таблиці, в яких ui + vi = cij, вважаючи, що u1 = 0.
u1 + v1 = 20; 0 + v1 = 20; v1 = 20
u1 + v2 = 16; 0 + v2 = 16; v2 = 16
u2 + v2 = 5; 16 + u2 = 5; u2 = -11
u1 + v3 = 13; 0 + v3 = 13; v3 = 13
u1 + v5 = 11; 0 + v5 = 11; v5 = 11
u3 + v5 = 15; 11 + u3 = 15; u3 = 4
u3 + v4 = 5; 4 + v4 = 5; v4 = 1
| v1 =20 |
v2 =16 |
v3 =13 |
v4 =1 |
v5 =11 |
|
| u1 =0 |
20[11] |
16[4] |
13[8] |
15 |
11[2] |
| u2 =-11 |
10 |
5[5] |
15 |
10 |
23 |
| u3 =4 |
25 |
20 |
5 |
5[6] |
15[4] |
Опорний план не є оптимальним, тому що існують оцінки вільних клітин, для яких ui + vi > cij
(3;3): 4 + 13 > 5; ∆33 = 4 + 13 - 5 = 12
Вибираємо максимальну оцінку вільної клітини (3;3): 5
Для цього в перспективну клітку (3;3) поставимо знак «+», а в інших вершинах багатокутника чергуються знаки «-», «+», «-».
| Завод №1 |
Завод №2 |
Завод №3 |
Завод №4 |
Завод №5 |
Запаси |
|
| Ферма №1 |
20[11] |
16[4] |
13[8][-] |
15 |
11[2][+] |
25 |
| Ферма №2 |
10 |
5[5] |
15 |
10 |
23 |
5 |
| Ферма №3 |
25 |
20 |
5[+] |
5[6] |
15[4][-] |
10 |
| Потреби |
11 |
9 |
8 |
6 |
6 |
Цикл наведено в таблиці (3,3; 3,5; 1,5; 1,3; ).
З вантажів хij стоять у мінусових клітинах, вибираємо найменше, тобто у = min (3, 5) = 4. Додаємо 4 до обсягів вантажів, що стоять у плюсових клітинах і віднімаємо 4 з Хij, стоять у мінусових клітинах. У результаті отримаємо новий опорний план.
| Завод №1 |
Завод №2 |
Завод №3 |
Завод №4 |
Завод №5 |
Запаси |
|
| Ферма №1 |
20[11] |
16[4] |
13[4] |
15 |
11[6] |
25 |
| Ферма №2 |
10 |
5[5] |
15 |
10 |
23 |
5 |
| Ферма №3 |
25 |
20 |
5[4] |
5[6] |
15 |
10 |
| Потреби |
11 |
9 |
8 |
6 |
6 |
Перевіримо оптимальність опорного плану. Знайдемо попередні потенціали ui, vi. по зайнятих клітинам таблиці, в яких ui + vi = cij, вважаючи, що u1 = 0.
u1 + v1 = 20; 0 + v1 = 20; v1 = 20
u1 + v2 = 16; 0 + v2 = 16; v2 = 16
u2 + v2 = 5; 16 + u2 = 5; u2 = -11
u1 + v3 = 13; 0 + v3 = 13; v3 = 13
u3 + v3 = 5; 13 + u3 = 5; u3 = -8
u3 + v4 = 5; -8 + v4 = 5; v4 = 13
u1 + v5 = 11; 0 + v5 = 11; v5 = 11
| v1 =20 |
v2 =16 |
v3 =13 |
v4 =13 |
v5 =11 |
|
| u1 =0 |
20[11] |
16[4] |
13[4] |
15 |
11[6] |
| u2 =-11 |
10 |
5[5] |
15 |
10 |
23 |
| u3 =-8 |
25 |
20 |
5[4] |
5[6] |
15 |
Опорний план є оптимальним, оскільки всі оцінки вільних клітин задовольняють умові ui + vi <= cij.
Мінімальні витрати складуть:
F(x) = 20*11 + 16*4 + 13*4 + 11*6 + 5*5 + 5*4 + 5*6 = 477
Задача 2.
Потреби хлібозаводу у борошні протягом періоду виробництва складають Z Вартість 1 тони борошна складає Ce Витрати на транспортування однієї партії борошна незалежно від її розмірів дорівнюють Cp Витрати на зберігання 1 тони борошна складають 12%-45,60 від вартості одиниці борошна. Представити графічне вирішення задачі – вибрати масштаб та побудувати графіки зміни Fр , Fu та F . Який розмір партії борошна буде економічно вигідніший для підприємства – 1000 тон або 2000 тон?
Таблиця 3
Вихідні дані для розрахунків
| Z |
150000 |
| Cp |
600 |
| Ce |
380 |
Розв’язок
Оптимальний розмір партії поставки та найменші сумарні витрати визначаємо за формулою Уілсона:
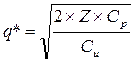 ;
; ![]() ;
;
Оптимальний розмір партії поставки буде таким:
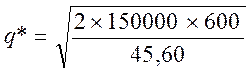 ;
;
q* = 1986,80 тонн
Мінімальні сумарні витрати на формування та зберігання запасів:
![]() ;
;
F*мін = 90598,01 грн
Згадаємо, що цільова функція F складається із суми двох функцій – Fp (показує залежність витрат на транспортування від розміру партії) і Fu (характеризує залежність витрат на зберігання партії від її розміру).
Для коректної побудови графіків Fр , Fu та F необхідно розрахувати і побудувати як мінімум по шість точок для кожної кривої, і хоча б дві точки для графіку прямої. Виберемо крок зміни аргументу q рівним 1000 т. У такому випадку отримаємо таблицю даних, за якими можна побудувати графіки:
Таблиця 4
Вихідні дані для побудови графіку витрат на управління запасами
| q |
1000 |
2000 |
3000 |
4000 |
5000 |
6000 |
| Fр |
90000 |
45000 |
30000 |
22500 |
18000 |
15000 |
| Fu |
22800 |
45600 |
68400 |
91200 |
114000 |
136800 |
| F |
112800 |
90600 |
98400 |
113700 |
132000 |
151800 |
Як видно із графіку (рис.1 витрати F досягають свого мінімального значення у точці на графіку (точка перетину Fр та Fu ), де є однаковими обидві суми витрат та темпи зміни Fр та Fu .
Результати вирішення моделі управління запасами графічним методом по рисунку 1: оптимальний розмір партії поставки приблизно 2000 тонн, мінімальні сумарні витрати на поставку та зберігання – близько 90600 грн.
Для підприємства економічно вигідніший розмір партії борошна буде 2000 тони, тому що витрати на 22200 грн. менші чим за партію 1000 тон
![]()
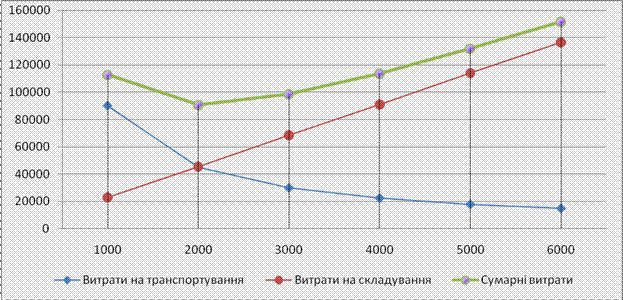
Рис 1. Графічне вирішення задачі управління запасами
Задача 3
Провести АВС- та XYZ-аналіз за приведеною базою даних. Зробити групування (виділити групи АХ, АY, AZ і
29-04-2015, 02:46
