Пересування пацієнтів у системі закладів охорони здоров’я (далі СМО – система медичного обслуговування) можна представити у вигляді графа, в якому вузли будуть відповідати місцям знаходження (обслуговування) їх, а “ребра” – пересуванню з одного місця до іншого. Топографія пересування кожного пацієнта буде залежати від особливостей поранення (захворювання або ураження), організаційних факторів тощо. Тому поранені, хворі хірургічного та терапевтичного профілю різного ступеня тяжкості, а також хворі тих чи інших класів, груп, підгруп і нозологічних форм захворювань розділяються на однорідні за медичними та евакуаційно-транспортними характеристиками групи (далі – категорії пацієнтів).
В результаті СМО може представлятися як мережа (рис. 4), вузлами (
) якої, в залежності від рівня деталізації, можуть бути групи відділень (кабінетів) закладів охорони здоров’я, підрозділи (відділення або кабінети) закладів або окремі лікарі (лікарсько-сестринські бригади), “ребрами” (
, 
) – потоки пацієнтів в дозволеному напрямку від вузла k
до вузла n
або навпаки:
, (1)
де: 
– кількість вузлів обслуговування.
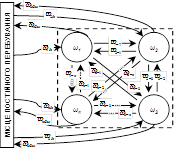Рис. 4. Принципова функціональна схема побудови мережевої моделі (графа) системи медичного обслуговування Для кожного вузла дозволяються окрім описаних вище потоків ще вхідний потік 
пацієнтів, вихідний потік 
(виписка пацієнтів назовні) та внутрішній потік пацієнтів 
з місця лікування у чергу на транспортування до інших вузлів (рис. 5).
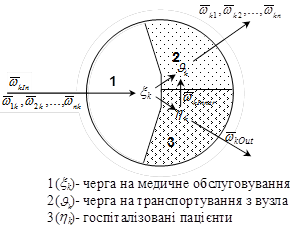Рис. 5. Принципова схема k
-го вузла медичного обслуговування Інтенсивності потоків пацієнтів в СМО (як внутрішніх так і зовнішніх) залежать від часу і вважаються випадковими величинами.
Для зручності комп’ютерної реалізації в математичній моделі використовувався дискретний спосіб завдання часу, позначеного як 
, 
, 
=1
доба, MaxDay
– тривалість часу (в добах), протягом якого здійснюється моделювання. Кожний проміжок часу
може бути розділений на Step
дискретних частин і, таким чином, може розглядатися як час 
, 
, 
, де Step
– так званий крок моделювання, котрий є цілим позитивним числом, частка від ділення на яке одиниці фактично означає частку проміжку часу
.
у вигляді випадкової функції з незалежними приростами. Інтенсивність такого нестаціонарного вхідного потоку пацієнтів 
на момент часу 
може бути визначена як: 
, (2)
де: 
– інтенсивність нестаціонарного адитивного потоку пацієнтів j
-ої категорії в момент часу ;
– момент дискретного часу
, 
; 
– кількість категорій пацієнтів.
Потік кожного вузла являє собою потік декількох категорій пацієнтів, що спрямовуються на вузол зовні, кожна категорія пацієнтів в моделі пересувається по унікальній послідовності вузлів обслуговування.
В свою чергу вхідний потік пацієнтів j
-ої категорії в момент часу до системи може бути представлений наступним чином:
, (3)
де: 
– частка пацієнтів j
-ої категорії від загальної кількості осіб з w
-м захворюванням або ураженням
– коефіцієнт втрат за окремим видом ураження або коефіцієнт захворюваності, що відповідає моменту часу , 
;
– початкова чисельність в момент часу g
-ї групи осіб (військова частина, угруповання військ, контингент населення та ін.), медичне забезпечення яких моделюється;
– кількість факторів ураження (видів зброї) та різновидів захворювань на мирний час.
З формули (3) виходить, що однорідні за своїми медичними характеристиками пацієнти, що належать до різних груп осіб, вважаються різними категоріями.
Вихідний потік пацієнтів з системи є нестаціонарним і являє собою суму усіх потоків . Його інтенсивність у момент часу 
(
) позначимо як 
:
, (4)
де: 
– інтенсивність вихідного потоку пацієнтів j
-ї
категорії з k
-го
вузла в момент часу ;
– кількість категорій пацієнтів, що спрямовуються на k
-й вузол.
Вихідний потік пацієнтів j
-ої категорії з k
-го вузла являє собою суму елементарних потоків виписки пацієнтів, що надходили в усі попередні моменти часу 
:
, (5)
, (6)
де: 
–
кількість пацієнтів j
-ої категорії, що надійшла на лікування у k
-му вузлі в момент часу q
(надходять з черги 
);
NFlowOut – кількість можливих станів пацієнтів (можливими станами є повне одужання, смерть та ін.);
–
імовірність виписки пацієнтів j
-ої категорії з k
-го вузла у стан f
в момент часу
;
–
імовірність виписки пацієнтів j
-ої категорії з k
-го вузла у стан f
в момент часу , який відповідає моменту часу
; 
, де 
– максимальний час лікування пацієнтів j
-ої категорії у k
-му вузлі (у добах);
, 
1
; (7)
b – індекс, що визначає вид моделі виписки, b = 0 для загальної нестаціонарної моделі, b = 1…7 для диференційованої нестаціонарної моделі (цими числами кодуються дні тижня, індекс b обчислюється відповідно до реальної дати надходження пацієнтів спеціальною функцією Delphi).
Інші формули математичної моделі описують переміщення пацієнтів з черги x
k
на медичне обслуговування в чергу 
на транспортування з вузла та в місце остаточного лікування, а також вплив факторів ризику на транспортні ресурси вузлів обслуговування та ресурси робочого часу на надання медичної допомоги.
Перевагою запропонованої математичної моделі є те, що вона дозволяє представляти потоки надходження та виписки пацієнтів як стаціонарні, так і складні нестаціонарні процеси. При цьому в моделі (формула 6) можливе представлення ймовірностей виписки (
) у вигляді аналітичних функцій або дискретного набору ймовірностей.
Розроблена математична модель була реалізована в комп’ютерних програмах “Модель системи надання медичної допомоги та етапного лікування” (“Model”) та “Модель закладу охорони здоров’я” (“Hospital”). Відповідно були розроблені алгоритми роботи та реляційна модель бази даних програмного забезпечення.
Важливим питанням комп’ютерної реалізації розробленої математичної моделі виявилась організація зберігання та обробки необхідної для моделювання інформації. Основні етапи переробки інформації під час моделювання та організація її зберігання знайшли відображення в розробленій інформаційній моделі, створеній згідно стандартів інформаційної технології SSADM. Згідно інформаційної моделі, моделювання представляється як комплекс інформаційних задач. Інформаційне моделювання дозволило встановити, що найголовнішою інформаційною задачею, яка повинна вирішуватись під час моделювання, виявилось не саме моделювання як обчислювальний процес, а задачі підготовки та відбору потрібної для моделювання інформації. Вирішальна роль якісного виконання цих інформаційних задач була підтверджена в експериментах по перевірці точності роботи моделі.
Вивчення точності роботи розробленої та реалізованої в комп’ютерній програмі “Hospital” математичної моделі по моделюванню завантаженості лікувальних закладів охорони здоров’я пацієнтами, проводилось за допомогою імітаційного та прогностичного моделювання роботи ГВКГ МО України.
Імітаційне завантаження ГВКГ МО України визначалося як результат взаємодії двох потоків: надходження та виписки пацієнтів. При імітації вхідного потоку хворих досліджувалась ефективність роботи двох моделей:1) стаціонарної – інтенсивність вхідного потоку дорівнювала середньої кількості хворих, що поступало щодня до ГВКГ МО України (66,26»66 пацієнтів);2)нестаціонарної – інтенсивність вхідного потоку визначалася на основі реальної кількості хворих, що поступали у ГВКГ МО України щодня.У якості нестаціонарної моделі використовувався реальний потік надходження пацієнтів у ГВКГ МО України починаючи з 26.01.2000 р.При імітації потоку виписки пацієнтів досліджувалась ефективність роботи таких моделей:1) стаціонарної – задавався середній термін лікування усіх пацієнтів (12,99»13 діб);2) загальної нестаціонарної – задавався розподіл ймовірності виписки у часі (загальний для усіх пацієнтів);3) диференційованої нестаціонарної – задавалися розподіли ймовірності виписки у часі, диференційовані по днях тижня надходження пацієнтів.Для імітаційного моделювання розподіли ймовірностей виписки, диференційовані по днях тижня надходження, були визначені на основі статистичних даних щодо термінів лікування усіх хворих, зареєстрованих в базі даних ГВКГ МО України.Прогностична точність роботи моделі оцінювалась нами наступним чином: на основі статичних даних щодо надходження та виписки пацієнтів у 2000-му, 2001-му та першій половині 2002-го року була прогнозована завантаженість госпіталю з 01.06.2002 р. до 31.05.2003 р.; для прогнозування використовувалась нестаціонарна модель вхідного потоку та диференційована нестаціонарна модель виписки. Розподіли ймовірностей виписки визначалися на основі статистичних даних щодо термінів лікування пацієнтів 11-го військового госпіталю, зареєстрованих станом на 03.06.2003 р., та пацієнтів ГВКГ МО України, що закінчили лікування та виписались до 01.06.2002 р. У якості потоку надходження використовувався реальний потік надходження пацієнтів з 02.06.2001 р. до 01.07.2002 р.
Варіанти змодельованого завантаження госпіталю пацієнтами наведено на рис. 6 та рис. 7.
З отриманих в результаті моделювання даних було визначено середню завантаженість госпіталю (табл. 4, де Хср. - середнє арифметичне, / D / - абсолютне відхилення між емпіричним і теоретично отриманим завантаженням) загалом і по днях тижня, яку порівняли з відповідною реальною (для імітаційного моделювання порівняння проводилось з 36-ої доби моделювання по 2825-у, що відповідає відрізку часу з 01.03.2000 р. до 20.10.2007 р., для прогностичного – з 1-ої до 366-ої доби, що відповідає відрізку з 01.06.2002 р. до 31.05.2003 р.).
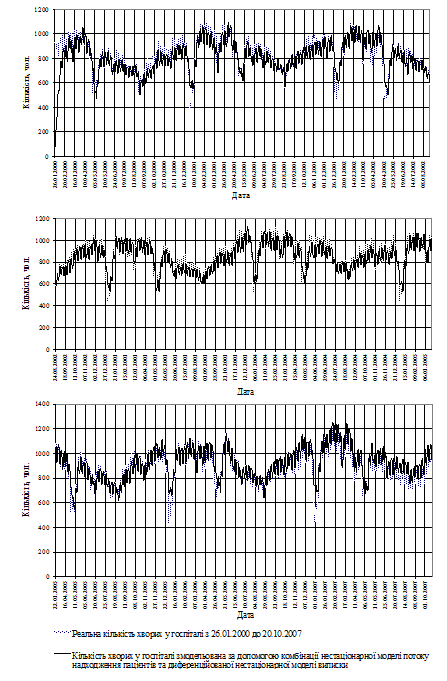
Рис. 6. Змодельоване (імітоване) завантаження пацієнтами ГВКГ МО України з 26.01.2000 р. до 20.10.2007 р. в порівнянні з реальним за цей же час
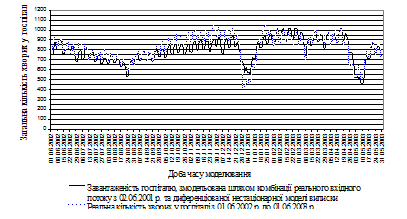
Рис.7. Реальна та змодельована (прогностична) завантаженість ГВКГ МО України хворими з 01.06.2002 р. до 01.06.2003 р.
У випадку імітаційного моделювання найменшу точність показали моделі:
– із стаціонарним вихідним потоком та стаціонарним вихідним (відносне відхилення склало 0,36%, середнє відносне абсолютне відхилення – 12,68%, варіаційне відхилення – 15,83%);
– із стаціонарним вхідним потоком та загальною нестаціонарною моделлю вихідного (відносне відхилення склало 0,51%, середнє відносне абсолютне відхилення – 12,704%, варіаційне відхилення – 15,84%);
– із сполученням стаціонарного вхідного потоку та диференційованої нестаціонарної моделі вихідного (відносне відхилення склало 0,96%, середнє відносне абсолютне відхилення – 12,62%, варіаційне відхилення – 15,68%).
Таблиця 4
Змодельована середня завантаженість госпіталю пацієнтами в порівнянні з реальною (n – обсяг вибірки)
| День тижня | Середня кількість хворих (X ср. ) отримана за допомогою: | |||||||
| прогностичного моделювання | імітаційного моделювання | |||||||
| n , дні | реальне X ср. | X ср. | / D / | n , дні | реальне X ср. | X ср. | / D / | |
| Понеділок | 52 | 850,19 | 829,68 | 20,51 | 398 | 885,94 | 884,77 | 1,17 |
| Вівторок | 52 | 865,21 | 838,88 | 26,33 | 398 | 899,33 | 897,90 | 1,42 |
| Середа | 52 | 868,46 | 845,95 | 22,52 | 399 | 908,70 | 907,26 | 1,44 |
| Четвер | 52 | 862,54 | 833,296 | 29,24 | 399 | 906,11 | 904,63 | 1,47 |
| П’ятниця | 52 | 781,36 | 755,74 | 25,63 | 399 | 814,47 | 813,52 | 0,94 |
| Субота | 53 | 773,96 | 752,57 | 21,396 | 399 | 802,72 | 802,00 | 0,71 |
| Неділя | 53 | 778,38 | 763,15 | 15,22 | 398 | 810,66 | 809,60 | 1,06 |
| Усі дні | 366 | 825,46 | 802,51 | 22,95 | 2790 | 861,13 | 859,95 | 1,17 |
Найбільш точною моделлю виявилась нестаціонарна по вхідному потоку і диференційована нестаціонарна по вихідному потоку (відносне відхилення склало 0,14%, середнє відносне абсолютне відхилення – 4,45%, варіаційне відхилення – 6,04%).
Показники, що відображають точність імітації, для інших моделей були наступні:
– для моделі із нестаціонарним вхідним потоком та стаціонарним вихідним відносне відхилення склало 0,066%, середнє відносне абсолютне відхилення – 8,599%, варіаційне відхилення – 10,69%;
– для моделі із сполученням нестаціонарного вхідного потоку та загальної нестаціонарної моделі вихідного відносне відхилення склало 0,23%, середнє відносне абсолютне відхилення – 5,52%, варіаційне відхилення – 7,17%.
Показники точності прогнозування були дещо меншими, що є цілком природно, і виявились наступними: відносне відхилення склало 2,78%, середнє відносне абсолютне відхилення – 6,16%, варіаційне відхилення – 7,699%.
При моделюванні за тривалий період (див. рис. 6) виявилось, що модель нестаціонарна по вхідному потоку і диференційована нестаціонарна по вихідному потоку дозволяє точніше врахувати достатньо великі абсолютні різниці завантаженості (сезонні - приблизно до 500 хворих, щотижневі - приблизно до 106 хворих), що зустрічаються під час реальної роботи госпіталю в повсякденних умовах.
Для порівняння розроблених підходів з існуючими традиційними методиками визначення потреби закладів охорони здоров’я у ліжковому фонді можна припустити, що добуток кількості населення, що підлягає медичному обслуговуванню, на госпіталізовану захворюваність з 01.03.2000 р. до 20.10.2007 р. буде аналогом кількості пацієнтів, що поступили в ГВКГ МО України за цей термін (184628 пацієнтів за 2790 днів або в середньому 66,175 пацієнт за добу). Якщо взяти за норматив роботи ліжка 340 діб за рік (це 93,15%), то норматив роботи ліжка за 2790 діб складе 2598,885 діб.
Тоді потреба у ліжковому фонді госпіталю складе: 
ліжка. Розрахункова середня зайнята кількість ліжок складе: 
, що практично відповідає реальному та змодельованому середньому завантаженню пацієнтами за цей же календарний період (реальне – 861,13 пацієнта).
Однак можна помітити, що госпіталь, як було відмічено раніше, завантажений нерівномірно: щорічно в літні місяці спостерігалося зниження завантаженості госпіталю до 500-700 хворих, а в січні-березні – підвищення приблизно до 1100 хворих, що значно вище визначеної потреби в ліжках. Також щорічно спостерігались короткочасні, але великі за розмахом коливання (зниження) завантаженості госпіталю на великі свята (амплітуда » 500-600 хворих), вплив яких на зменшення середніх показників не викликає сумнівів. Суттєве значення також мали щотижневі статистично значимі регулярні коливання завантаженості госпіталю, які, відповідно, призводять до статистично значимого зниження середньої завантаженості госпіталю як за реальними даними, так і за результатами моделювання. Всі перелічені особливості знайшли відображення у відносно великому середньому квадратичному відхиленні (див. табл. 2).
Отже, розрахована на основі середніх показників завантаженості потреба госпіталю у ліжках, безсумнівно, не відображає достовірно реальну картину внаслідок її заниження, яке виникає із-за перерахованих регулярних сезонних, щотижневих та на великі свята коливань.
Таким чином, тільки метод математичного моделювання з комп’ютерною реалізацією дозволив зімітувати ці коливання і, відповідно, зімітувати екстремуми завантаженості госпіталю хворими, що робить його найбільш прийнятним засобом для вирішення проблеми планування потреби в ліжках.
ВИСНОВКИ
В дисертаційній роботі на підставі отриманих результатів досліджень, а також з урахуванням даних літературних джерел, було запропоновано оригінальне наукове вирішення задачі визначення потреби закладів охорони здоров’я в ліжках, що дозволяє суттєво удосконалити процес управління лікувально-профілактичним (лікувально-евакуаційним) забезпеченням Збройних Сил України.
1). Доведено, що розроблена в дисертаційному дослідженні математична модель дозволяє досить точно відтворити завантаження лікувальних закладів охорони здоров’я пацієнтами, його щотижневі та сезонні коливання, внаслідок чого з’являється можливість визначати потребу лікувальних закладів охорони здоров’я у ліжковому фонді за принципом орієнтування на максимально-необхідну ліжкову місткість.
2). Встановлено, що моделювання з усіма сполученнями моделей вхідного та вихідного потоку дозволяє точно визначити середню завантаженість лікувального закладу пацієнтами (різниця змодельованого і реального середнього завантаження була <1% і складала 0,066%-0,96% залежно від варіантів сполучення).
3). Визначено, що найменша точність притаманна моделям із сполученням стаціонарного вхідного потоку та стаціонарного вихідного (середнє відносне абсолютне відхилення склало 12,68%), найбільш точною є модель нестаціонарна по вхідному потоку і диференційована нестаціонарна по вихідному потоку (середнє відносне абсолютне відхилення склало 4,45%). Дещо менш точними (друге місце) є моделі із сполученням нестаціонарного вхідного потоку та загальної нестаціонарної моделі вихідного (середнє відносне абсолютне відхилення склало 5,52%). Інші моделі потенційно мають меншу точність.
4). Встановлено важливі закономірності надходження та виписки пацієнтів у лікувальних закладах охорони здоров’я на мирний час, а саме: підпорядкованість статистичному закону нормального розподілу випадкової величини частотних характеристик кількості пацієнтів, що надходили та виписувались в різні дні тижня. Встановлені закономірності обумовлюють доцільність застосування в моделях нестаціонарної моделі вхідного потоку та диференційованої нестаціонарної моделі вихідного потоку пацієнтів.
5). Встановлена і кількісно оцінена щотижнева динаміка зміни потоку виписки пацієнтів, яка проявляється у зменшенні інтенсивності виписки пацієнтів на початку робочого тижня (у понеділок-вівторок виписувалось 28,92-29,92% пацієнтів), збільшенні наприкінці (в четвер-п’ятницю виписувалось 46,59-48,11% пацієнтів), та різкому зменшенні у вихідні дні (виписувалось 6,35-7,54% пацієнтів).
8-09-2015, 22:29