Пассажирские перевозки 2

border="1">

Размер пассажиропотока в одном направлении Q_{i max} , (пасс./ч)

Интервал движения на маршруте 1 (мин)

Количество автобусов на 1 км автобусной транспортной сети

До 750

8,0

0,5

751 – 1500

4,0

1,0

1501 – 2250

2,7

1,5

2251 – 3000

2,0

2,0

3001 – 3750

1,6

2,5

3751 – 4500

1,3

3,0

Свыше 4500

1,0

4,0

По рекомендациям A.M. Большакова для выбора вместимости автобуса можно использовать выражение:

, или q _н = Q_imax *I . (9)

где: Q_imax - максимальная величина пассажиропотока за час (табл.1 или 2)

Ч - частота движения, (авт./час.). Величина обратная интервалу, т.е. (10)

Используя данные таблицы 4 видно, что для нашего примера I =4 мин., так как с 17до 18 час Q imax .– 821 пасс/час. Тогда:

Ч=1/4, или Ч=60/4=15 авт/час.

Тогда: q_Н = 821/15=54,7, или q_Н =821*4/60=54,7

Примечание 4 мин = 4/60=0,07 часа.

По рекомендациям И.С. Ефремова для выбора вместимости автобуса используется выражение:

(11)

где γ_пик - коэффициент использования вместимости автобуса для часов «пик» (γ _пик =0,78)

из выражения (11):

(12)

Следовательно, для нашего примера:

Таким образом, по методике НИИАТ требуется автобус вместимостью 85 пассажиров, а расчеты по методикам И.С. Ефремова и A.M. Большакова показывают, что на данном маршруте необходимо использовать автобус номинальной вместимостью 65 пассажиров.

В дальнейших наших расчетах принимаем автобус номинальной вместимостью 63 пассажиров. ЛАЗ-42021.

Таблица 4 - Номинальная вместимость автобусов различных марок

Марка автобуса	Номинальная вместимость () пасс.
ПАЗ-3205	34
ЛАЗ-42021	63
Альтерна-4216	80
ЛиАЗ-5293 Полуизкопольный	100
МАЗ 203 Низкопольный	102
Волжанин Сити Ритм Полуниз	104
VDL НЕФАЗ 52997 Полунизкопольный	104
MAN NL 263/313: 15-метровый, низкорамный,	111
ЛиАЗ-5256	116
ЛиАЗ-52922 Низкопольный	120
МАЗ 204	204
Neoplan CityLiner 1116 Туристический	51+1+1

ПРИМЕЧАНИЕ: Максимальная вместимость автобуса может быть принята на 30% больше номинальной вместимости. Кроме туристичесеого.

2.2 Расчет потребного количества автобусов

Расчет потребного количества автобусов для каждого часа суток выполним для автобуса вместимостью 63 пассажиров по выражению:

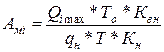(13)

· Q_imax –Расчетное значение пассажиропотока (пасс.) для данного часа суток (таб. 2).

· Т_о – время оборота на маршруте. (час.);

· К_вн – коэффициент внутри-часовой неравномерности пассажиропотока (принимается величина от 1,01 до 1,2, максимум – 1,3);

· q _н –вместимость выбранного типа автобуса (количество человек)

· Т = 1 т.е. период времени, за который получена информация о пассажиропотоке один час

· К_н – коэффициент надежности (регулярности), принимается от 0,90 до 0,99.

Время оборота определим по выражению:

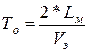(14)

Эксплуатационную скорость (V э ) рассчитаем из равенства:

L м =0,5 * A_{м i max} * V э .* I. (15)

От сюда:

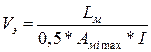(16)

Максимальное количество автобусов предварительно определим по отношению:

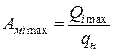(17)

А_mimax =821/63=13

По выражению (15) получим:

V_Э =9,7/0,5*13*0,07=17 км/час

Тогда из равенства (14):

Т_О =2*9,7/17=1,1 час

Используя выражение (5) в дальнейших расчетах, для нашего примера получим:

………………………………….

…………………………….и т.д.

При получении дробных величин A_мi следует округлять до целого числа; если дробная часть меньше половины, то она отбрасывается, если больше половины, то число округляется до целого в большую сторону. Для часов «пик» номинальную вместимость автобуса (q _н ) в выражении (13) можно увеличить до максимальной вместимости (табл.4).

Расчеты по формуле (13) необходимо выполнить для автобусов большой (A^бв _мi ) и малой вместимости (A^мв _мi ) Полученные данные заносим в таблицу 1. В сумме автобусы большой вместимости должны затратить 57 автомобиле часов, автобусы малой вместимости – 181 (табл.1).

2.3 Окончательный выбор типа автобуса по вместимости

На заключительном этапе следует доказать целесообразность использования для данного маршрута автобуса малой, или большой вместимости. Для этого необходимо использовать графо-аналитический метод.

Краткая сущность этого метода. Предварительно выбранные выше типы автобусов сравниваются по себестоимости перевозок. Для нашего примера имеем автобус малой вместимости - 60 пассажиров (А ^мв ) и автобус большой вместимости - 80 пассажиров (А^бв ).

На первом этапе выполняется построение номограммы, по которой графически определяется общее число двух сравниваемых автобусов на маршруте по часам суток.

На втором этапе графически определяется необходимое число сравниваемых автобусов по часам суток по условию максимального временного интервала движения.

Третий этап (рис.1) позволяет сравнить работу автобусов различной вместимости по себестоимости перевозок. В левой части номограммы представлены зависимости себестоимости сравниваемых автобусов от величины статических коэффициента использования их вместимостей. В правой части номограммы представлены колебания статических коэффициентов использования вместимостей по часам суток. Кривая 0-0 - малой вместимости. Кривая 1-1 – большой вместимости.

Для сравнения эффективности их работы на данном маршруте по себестоимости необходимо построить две горизонтальные линии (пунктирные линии на рис.1) характеризующие значение коэффициента использования вместимости (γ _сс ) сравниваемых автобусов в часы «пик» рассчитанные по формуле:

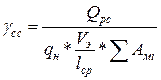(18)

Где: Q рс - расчетное значение (Табл. 1)

q _н – номинальная вместимость автобуса,

V э - эксплуатационная скорость автобуса,(км/час)

l _ср – средняя дальность поездки одного пассажира, (км)

∑А_{м i} –количество часов работы автобусов на маршруте за сутки (20 часов для нашего примера)

Для нашего примера, подставленные значения в выражение 18, при одинаковой эксплуатационной скорости, дают следующие числовые величины статических коэффициентов использования вместимости сравниваемых автобусов для часов «пик»:

для автобуса малой вместимости;

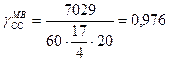
для автобуса большой вместимости;

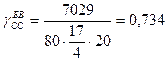
Результаты расчетов и графические построения на рис.10 говорят о том, что себестоимость перевозок автобусом большой вместимости составляет около 9 руб. за один пас-км, а малой – более 10 руб. (вертикальные пунктирные линии на рис.1)

Правильность выбора подтвердить расчетом по формуле:

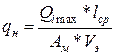(11)

Таким образом, в дальнейших расчетах необходимо принять автобус номинальной вместимостью 63 – 200 пассажиров.

В соответствии со справочными данными и таблицы 4 на данном маршруте рекомендуется эксплуатация автобуса марки ЛАЗ-42021, или автобуса марки МАЗ – 204.

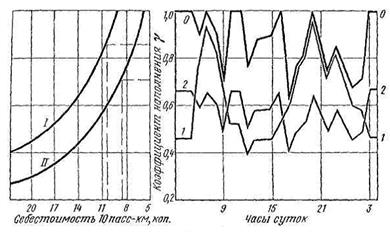
Рис. 10 Сравнение работы автобусов различной вместимости по себестоимости перевозок.

I –автобус малой вместимости (60пас.). II –автобус большой вместимости (80пас.)

Горизонтальные пунктирные линии соответственно γ ^мв _сс =0,976 и γ ^бв _сс =0,734.

2.4 Построение диаграммы «максимум»

Построение диаграммы "максимум" производится следующим образом. По оси X откладываем часы суток работы автобусов на маршруте (Т_сут ). По оси Y – потребное количество автобусов (A^бв _мi ) в каждый час по расчетным данным табл.1. Пример построения показан на рисунке 11.

Линия "max." наносится на диаграмму с учетом коэффициента дефицита (К_Д ):

A_м.max = A_м.imax ×*К_Д (20)

где К_Д – коэффициент дефицита (принимается от 0,8 до 0,9.)

Дефицит автомобилечасов выше линии "max ." отбрасывается и в дальнейших расчетах не учитывается (4 часа).

В нашем примере A_max = 17×0,8=13. Это значение фиксируем линией “max ” на диаграмме "максимум" рис.11.

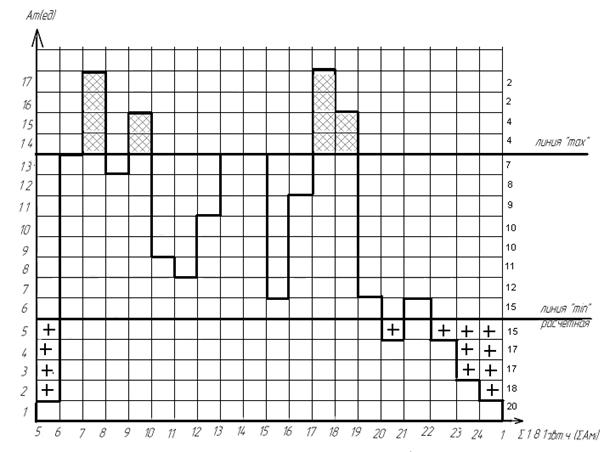
Рисунок 11 - Диаграмма «max»

Линия « min ». Значение абсолютной величины, где проходит линия "min " на диаграмме, определяется по выражению

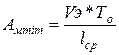(21)

Где:

· V _э – эксплуатационная скорость автобуса на маршруте (км/ч);

· Т_о- - время оборота автобуса на маршруте (час);

· l _cp – средняя дальность поездки одного пассажира (км), принимается из расчетов по лабораторной работе № 1

Если значение линии "min " меньше 0,5×A_max , то к площади диаграммы необходимо добавить автомобилечасы (t ₊ ), которые находятся между линией "min " и контуром основания диаграммы (рис. 3). Если значение линии "min " больше 0,5*×A_max ,то линия "min " в расчет не принимается. Для нашего примера

Значение линии «min » наносим на диаграмму "максимум"(сплошная линия "min "на рис. 11)

В нашем примере, А_{м mim} =5. Следовательно, она в расчет принимается. (рис.3)

Количеством транспортной работы на маршруте (Т_м в автомобиле-часах) является площадь откорректированной диаграммы "максимум" по условию линий "min " и "max ".

Суммарное количество транспортной работы на маршруте (Т_м ) определяется по выражению:

Т_м = ∑Ам_i – t _Д + t ₊ (22)

При t ₊ =13 Т_м =181 – 12 + 13 =182 авт.ч (рис.11)

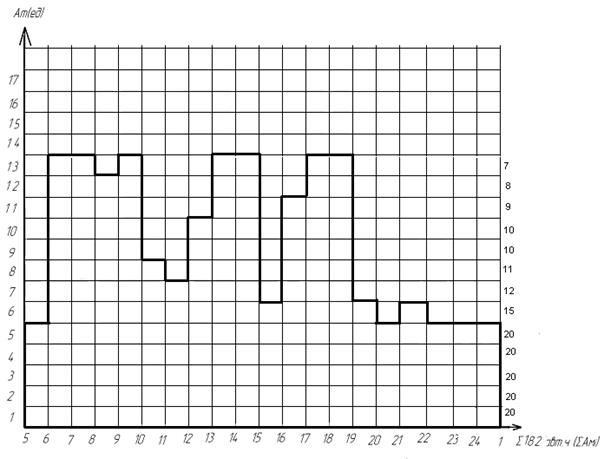
Рисунок 12 - Откорректированная диаграмма «max» при А_mim =5

Интервал движения автобусов (I _i ) в каждый час суток определится из отношения:

(23)

Частота движения (Ч) – это величина, обратная интервалу, то есть количество автобусов в час. Полученные значения расчетов заносим в
таблицу 2.

На всех диаграмм, например рисунки 3 и 4 по оси Y мы имеем данные о необходимом количестве работающих на маршруте автобусов в каждый час суток. Количество выходов это число строк откорректированной диаграммы "max ". Для нашего примера количество выходов равно 13. По строке (ось X ) имеем продолжительность работы каждого из 13 выходов в течение суток. Количество автомобилечасов (площадь диаграммы), подсчитанное по столбцам всегда будет равно количеству автомобилечасов подсчитанное по строке. Для нашего примера на рис.12 182 = 182

3 Определение рациональных режимов работы выходов и водителей (графоаналитический расчет)

Цель графоаналитического расчета – определение минимального необходимого набора режимов работы транспортных единиц на маршруте при достижении наименьших общих затрат машино-часов.

Графическое построение основывается на следующих принципах:

- не изменяя суммарного числа занятых клеток по каждому столбцу и используя метод зеркального отображения с перенесением фрагмента диаграммы с одной линии основания на другую, необходимо добиваться максимально возможного приближения числа занятых клеток по каждой строке к предпочтительной величине продолжительности работы ;

- следует стремиться в возможных пределах к максимальному упрощению получаемых геометрических фигур-фрагментов диаграммы «максимум» - к достижению простейших, прямоугольной формы каждого фрагмента диаграммы, соответствующего группе выходов той или иной классификации.

3.1 Первый вариант графоаналитического расчета

По параметрам и характеристикам диаграммы «максимум» проанализировать три из различных возможных варианта различных форм для организации труда водителей и выходов.

1. Первый вариант ориентирован на шестидневную рабочую неделю водителей маршрута со средней продолжительностью работы одной смены Δt =6,83 часа.

2.Второй вариант предполагает пятидневную рабочую неделю водителей маршрута со средней продолжительностью работы одной смены Δt =8,2 часа.

3. Третий вариант ориентирован на работу водителей по графику, который предусматривает выходной день через каждые две отработанные смены со средней продолжительностью Δt =8,7 часа. При этом за каждым двухсменным выходом закрепляется три водителя, а ежедневно на выходе работают два водителя.

Исходные данные для всех трех рассматриваемых вариантов является диаграмма «max». Значения A_max , q_H , l_cp , Vэ, T_o ,Т_м , t₊ принимаются по данным ЛР № 1 и №2.

Для первого и второго вариантов значения минимальной и максимальной продолжительности работы одной смены, принимается соответственно, Δt_mm = 3 часа, Δt_max = 9,5часа. Минимальная продолжительность обеденного перерыва в первую и вторую смены соответственно Δt₁ =0,6 часа, Δt₂ = 0,5 часа. Время нулевого пробега по каждому выходу: t_о = 0,5 часа.

Для третьего варианта исходные данные принимаются такие же, как в первом и втором варианте, за исключением Δt_min = 7,0 час, Δt_max = 10 часов

Решение задачи и поиск рационального режима работы водителей и выходов осуществляется путем аналитических расчетов и графических построений по методике Г.А. Варелопуло.

Выполняется построение откорректированной диаграммы «max» по условию линий максимум и минимум (рисунок 12).

На рисунке 13 представлена откорректированная диаграмма максимум, по которой будут производится построения.

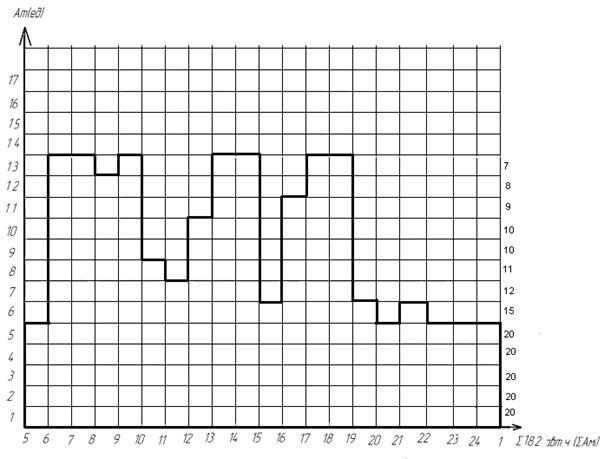
Рисунок 13 – Откорректированная диаграмма максимум, по которой будут производиться построения

Рассчитывается и определяется классификация выходов по сменности и выполняется построение диаграммы с линией деления по сменности и резервными зонами для отдыха водителей и питания.

Рассчитывается и определяется классификация выходов по сменности, в условиях применения единого для всех водителей графика работы, т.е. определяем количество выходов, которые должны работать в одну, две или три смены, по выражению:

(24)

Из рисунка 5 имеем: Т_М = 181; =13; =12; a = 0; A_max = 13; =6,83.

Тогда:

Принимаем = 0

Результат вычисления по выражению (24) может иметь значение: со знаком плюс, минус, или ноль.

Значение ΔА = 0 говорит о том, что все выходы должны работать в двух сменном режиме. В этом случае графические построения для всех выходов выполняются между основанием диаграммы и линией «max».

Знак минус требует организации работы выходов в две смены. Цифра при знаке минус указывает, сколько должно быть одно сменных выходов. Остальные выходы должны работать в две смены. В этом случае графические построения выполняются отдельно по каждой группе выходов. Для двух сменных между основанием диаграммы и линией деления по сменности. Для одно сменных выходов между линией деления по сменности и линией «mах».

Знак плюс требует организации работы выходов в три смены. Цифра при знаке плюс указывает, сколько должно быть трех сменных выходов. Остальные выходы должны работать в две смены. В этом случае графические построения выполняются отдельно по каждой группе выходов. Для трех сменных между основанием диаграммы и линией деления по сменности. Для двух сменных между линией деления по сменности и линией «mах».

Выполняется построение диаграмма «max» c линией деления по сменности и резервными зонами автомобилечасов для перерыва на отдых и питание (обед). Диаграммы представлены на рисунках 14 и 15.

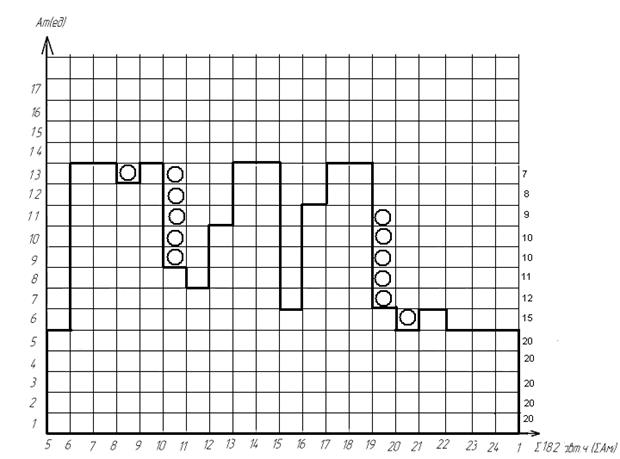
Рисунок 14 – Распределение перерывов на отдых и питание водителей

На рисунке 15 дана диаграмма с включенными обедами.

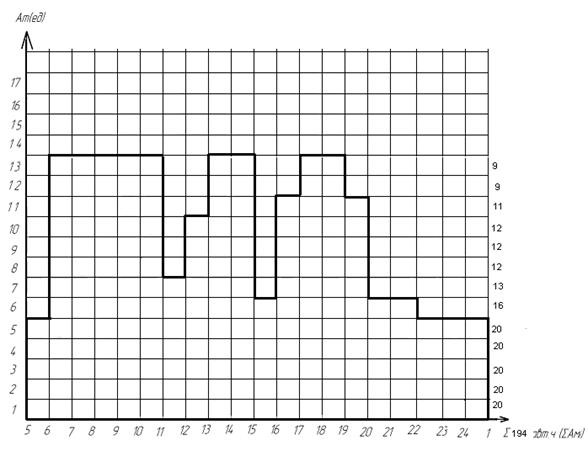
Рисунок 15 – Диаграмма с включенными обедами

Мы приняли, что все выходы двухсменные (рисунок 16).

Далее выполняем промежуточные (поисковые) графические построения. Для этого используется метод зеркального отображения фрагментов фигур диаграммы. Целью поиска является определение минимальной разницы между max и min величиной продолжительности работы выходов в каждой группе по режиму работы. Конфигурация диаграммы, где эта разница минимальна, является оптимальной геометрической фигурой исходя из равных условий работы водителей.

На рисунке 17 изображена диаграмма с заштрихованными секторами А и Б. Нам необходимо будет зеркально отображать эти сектора так, чтобы разница между max и min величиной продолжительности работы выходов в каждой группе по режиму работы была минимальной.

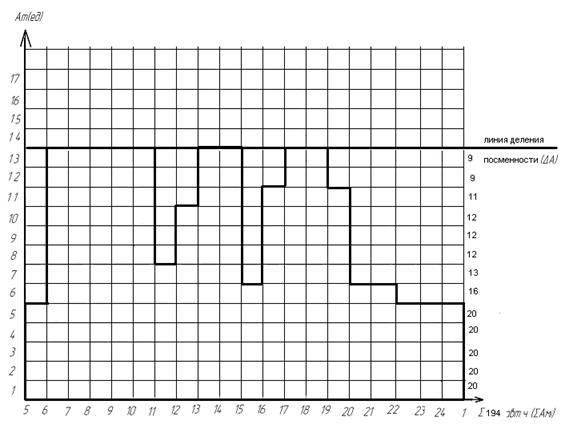
Рисунок 16 – Диаграмма с включенными обедами и линией деления по сменности

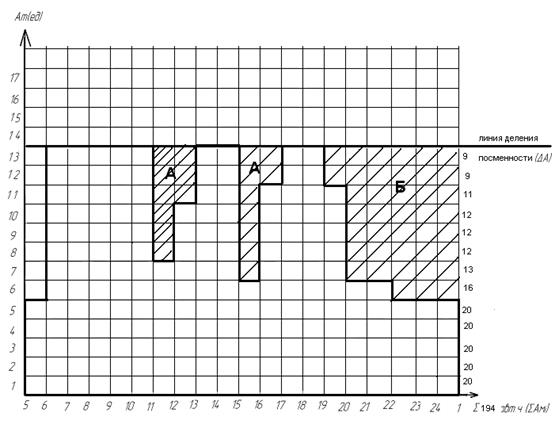
Рисунок 17 – Первый шаг поиска оптимальной конфигурации геометрической фигуры диаграммы

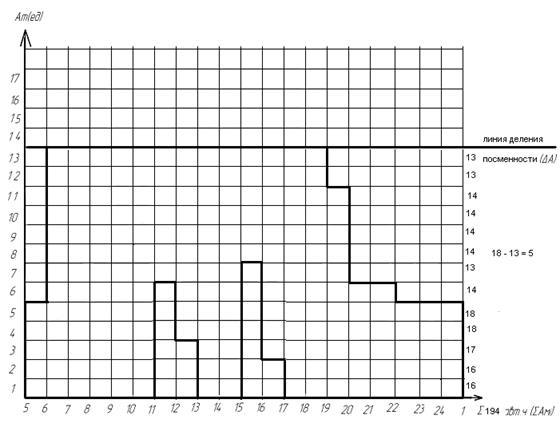
Рисунок 18 – Второй шаг


8-09-2015, 12:10