6. Определяем необходимое количество автомобилей для работы на маршруте
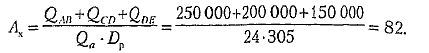
7.Определяем суточный пробег автомобиля, км
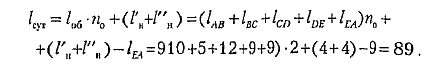
8.Коэффициент использования пробега на маршруте
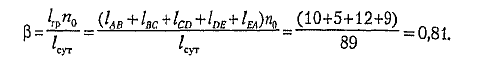
4. Применение математических методов для организации материалопотока.
Применение математических методов и моделей в логистике необходимо в тех случаях, когда проблема сложна и решить ее простейшими методами на основе опыта работы невозможно. В этом случае непродуманное и научно не обоснованное решение может привести к серьезным последствиям. Примеров этому в нашей жизни имеется не мало, в частности, в логистике и экономике. Использование математических методов и моделей позволяет логисту осуществить выбор оптимальных или близких к ним вариантов решений по определенным критериям. Естественно, эти решения научно обоснованы, и логист, принимающий решения, может руководствоваться ими при выборе окончательного решения.
В этом разделе будут рассмотрены некоторые математические модели, которые могут быть использованы логистом при принятии логистических решений при продвижении материалопотока автомобильным транспортом.
На автомобильном транспорте методом линейного программирования решают такие задачи:
- отыскание оптимального числа ездок автомобилей на маршрутах при установленном времени пребывания в наряде (задача на минимальные потери рабочего времени);
- отыскание оптимального варианта закрепления получателей за поставщиками однородной продукции (задача на минимум пулевых пробегов);
- составление рациональных маршрутов работы подвижного состава — увязка ездок (задача на минимум холостых пробегов);
- организация развозочных и сборочных маршрутов (задача па определение минимального пробега при объезде грузопунктов);
- распределение подвижного состава и погрузочно-разгрузочиых средств по маршрутам работы (задача па максимальное использование рабочего времени автомобилей и погрузочно-разгрузочиых механизмов и др.).
Все перечисленные задачи базируются на математическом моделировании изучаемого процесса, т. е. на описании количественных закономерностей этого процесса, с помощью математических выражений (математической модели). Математическая модель, как уже было сказано, является абстрактным изображением реального процесса и в меру своей абстрактности может его характеризовать более или менее точно.
Одной из задач в логистической системе является разработка стратегии и логистической концепции построения модели транспортного обслуживания потребителей и фирм. Эта стратегия основывается на расчете рациональных маршрутов перевозки и составлении оптимальных графиков (расписаний) доставки продукции потребителям, т. е. отвечает на вопросы, когда, сколько и в какое время должны быть доставлены грузы.
Вариантами организации движения автомобиля могут быть: маятниковый маршрут с обратным порожним пробегом или развозоч-ный маршрут при перевозке мелкопартиониых грузов потребителям. Подробно рассмотрим организацию этих маршрутов.
4.1. Маятниковый маршрут с обратным порожним пробегом.
На практике при планировании работы автомобилей по маятниковым маршрутам с обратным холостым пробегом руководствуются единственным правилом: последний пункт разгрузки автомобилей должен быть как можно ближе к автохозяйству. При соблюдении этой основанной на здравом смысле рекомендации обеспечивается минимум пробега без груза. Анализ рассматриваемой задачи методом линейного программирования показал, что такое решение совсем неочевидно. Для доказательства рассмотрим пример.
Пример 5.
Допустим, что с базы А необходимо доставить продукцию потребителям Б1 и Б2. К обоим потребителям автомобиль может сделать за время в наряде две ездки. Необходимо составить маршрут движения автомобиля, обеспечивающий минимум порожнего пробега.
Условия задачи, схема размещения потребителей, на примере решения которой составляется маршрут движения, приведены на рис.9.

Рис. 9. Схемы размещения потребителей
Решение.
При решении этой задачи могут возникнуть два случая:
1)продукция поставляется в пункт Б2, а затем в Б1, из Б1 автомобиль поступает в АТП (пункт Г);
2)продукция поставляется в пункт Б2, а потом в Б1, из Б1 автомобиль возвращается в АТП (пункт Г).
Для выбора варианта перевозки продукции произведем расчет коэффициента использования пробега автомобиля и полученные значения сведем в табл. 3.
| Показатель | Вариант I | Вариант II |
| Пробег, км: | ||
| общий | 103,0 | 97,5 |
| порожний | 57,0 | 51,5 |
| груженый | 46,0 | 46,0 |
| Коэффициент использования пробега | 0,44 | 0,47 |
Таблица 3. Коэффициент использования пробега автомобиля β по вариантам
Как видно из таблицы, наиболее эффективен второй вариант, поскольку коэффициент использования пробега во втором случае выше, чем в первом.
Однако если руководствоваться правилом, что наименьший пробег достигается, когда первый пункт погрузки и последний пункт разгрузки находятся поблизости от автотранспортного предприятия, целесообразен первый вариант, Чтобы проверить правильность выбора, решим задачу математическом методом.
Задача составления рациональных маршрутов, обеспечивающих минимальный порожний пробег транспортных средств, сводится к следующей задаче линейного программирования:
минимизировать линейную формулу
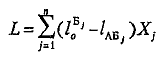
При условиях
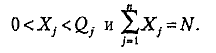
Допустим, что пункты назначения занумерованы в порядке возрастания разностей ![]()
![]()
Тогда оптимальное решение таково:
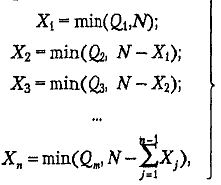
где L — порожний пробег, км;
l Б j 0 — расстояние от пункта назначения Бj , до автотранспортного предприятия (второй нулевой пробег), км;
l АБ - расстояние от А до Бj (груженый пробег), км;
j — номер (индекс) потребителя (j= 1, 2, … п);
Xj — количество автомобилей, работающих на маршрутах с последним пунктом разгрузки Бj ;
N — число автомобилей, работающих на всех маршрутах;
Qj — объем перевозок.
![]() Решая эту задачу, мы должны знать, что наилучшее решение получается при такой системе маршрутов, когда максимальное число автомобилей заканчивает работу в пунктах назначения с минимальными разностями т. е. второго нулевого и груженого пробегов.
Решая эту задачу, мы должны знать, что наилучшее решение получается при такой системе маршрутов, когда максимальное число автомобилей заканчивает работу в пунктах назначения с минимальными разностями т. е. второго нулевого и груженого пробегов.
Для решения задачи необходимо исходные данные записать в специальную таблицу, с помощью которой произвести все необходимые вычисления по составлению маршрутов (табл. 4).
| Пункт назначения | Количество груженых ездок | Столбец разностей | ||
| Б1 | Q1 | |||
| Б2 | Q2 | |||
| … | ||||
| Бj | Qj | |||
| … | ||||
| Бn | Qn | |||
Таблица 4. Исходные данные.
![]() Для каждого пункта назначения, т. е. по каждой строке, рассчитывают алгебраические разности , которые записывают в соответствующие клетки столбца разностей.
Для каждого пункта назначения, т. е. по каждой строке, рассчитывают алгебраические разности , которые записывают в соответствующие клетки столбца разностей.
Рассмотрим применение предложенного алгоритма на примере, воспользовавшись исходными данными, приведенными на рис. 9.
Исходя из этих условий составляем таблицы объема перевозок (ездок) и расстояния перевозок (табл. 5, 6).
| Пункт отправления | Пункт назначения | |
| Б1 | Б2 | |
| А | 2 | 2 |
Таблица 5. Объем перевозок(ездки)
| Пункт отправления | Автохозяйство | Пункт назначения | |
| Б1 | Б2 | ||
| А | 13 | 8 | 15 |
| Г | — | 6 | 7,5 |
Таблица 6. Расстояние перевозок, км.
Составляем рабочую матрицу условий (табл. 7), используя данные таблиц, и решаем ее.
| Пункт назначения | А (пункт отправления) |
Столбец разностей (оценки,) | ||
| Б, | 6 | 2 | 8 | -2 |
| Б, | 7,5 | 2 | 15 | -7,5 |
Таблица 7. Рабочая матрица условий.
Наименьшую оценку (-7,5) имеет пункт Б2 , в который нужно сделать две ездки. Принимаем его последним пунктом маршрута А — Б2 - Г, т. е. получаем маршрут варианта II.
Расчет экономической эффективности применения экономико-математических методов при маршрутизации перевозок определяют по формуле:
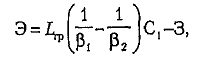
где LГР - пробег подвижного состава с грузом, тыс, км;
β1, β2 - коэффициенты использования пробега, вычисленные до применения ЭВМ и на ЭВМ;
С1 - средние затраты на i км пробега подвижного сэстава, коп.;
3 — расходы на выполнение расчетов по решению задач, тыс. руб.
4.2. Развозочный маршрут при перевозке мелкопартионных грузов потребителям.
Постановка задачи. Заданы пункты потребления Xi ( i =1,2,…,n). Груз необходимо развезти из начального пункта Х0 (склад) во все остальные X i (потребители). Потребность пунктов потребления в объеме поставки составляет q 1 , q 2 ,…, qn . В начальном пункте имеются транспортные средства в количестве d грузоподъемностью Q1 ,Q2,…, Qd .
Известно также расстояние перевозки lij между потребителями.
При решении задачи необходимо учитывать, что количество транспортных средств d
должно быть больше, чем пунктов потребления n
(
d
> п);
в начальном пункте Х0
(склад) количество продукции должно быть больше или равно сумме потребностей всех потребителей ![]() . Каждый пункт потребления обслуживается
. Каждый пункт потребления обслуживается
подвижным составом одного типа (автомобиль грузоподъемностью 2,5 т); груз 2-го класса; γ=0,8.
Для каждой пары пунктов (X i ,.... Хп ) определяем расстояние перевозки lij . Это расстояние должно быть больше или равно нулю, т. е. lij >0.
Схема размещения пунктов и расстояния между ними приведены рис. 10.
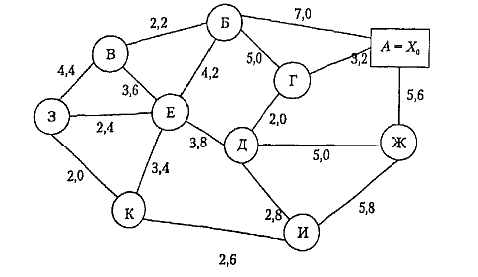
Рис. 10. Схема размещения пунктов и расстояния между ними
Требуется найти т замкнутых путей l 1 , l 2 ,… lm из единственной общей точки X0 и так, чтобы выполнялось условие:
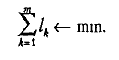
Заключение.
Список литературы.
29-04-2015, 02:07
