где

К_B - константа скорости встраивания молекул в кристалл;

n - эмпирическая постоянная.

• Оба процесса протекают с соизмеримыми скоростями:

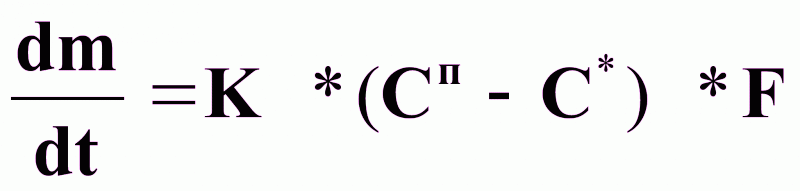(3),

где

К - общий коэффициент скорости процесса, определяемый из соотношения:

.

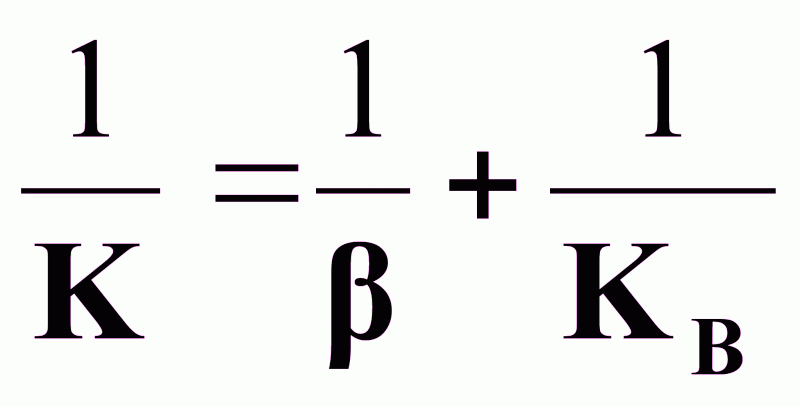Учитывая, что К=f(, K_B), а =f(n), в целом можно считать:

.

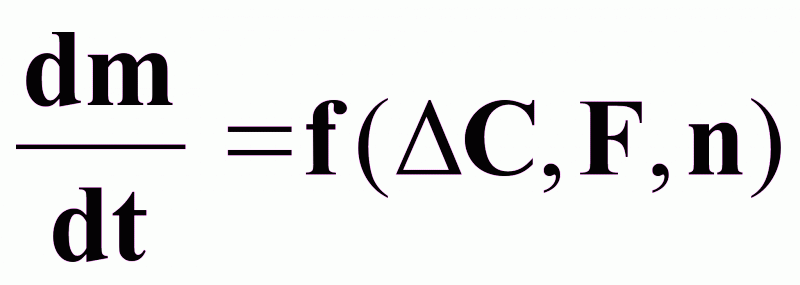Таким образом, скорость роста кристаллов определяется поверхностью кристалла, движущей силой процесса и скоростью мешалки.

Объект управления

Изогидрический кристаллизатор непрерывного действия с мешалкой.

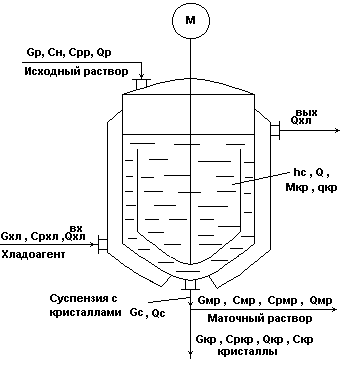
Рис.5.

В схеме принято:

G_с=G_мр+G_кр; _мр = _кр = _с =;

С_кр = 1, т.е. кристаллы чистые.

Работа объекта

Исходный горячий насыщенный раствор подается сверху в аппарат, где охлаждается с помощью хладоносителя, подаваемого в рубашку и становится пересыщенным.

В результате пересыщения раствора и при интенсивном перемешивании происходит кристаллизация целевого компонента из раствора с образованием кристаллов (М_крG_кр).

При этом концентрация раствора понижается и оставшаяся жидкая фаза G_мр в смеси с G_кр в виде потока суспензии G_c выводится из процесса.

Показатель эффективности процесса - диаметр кристаллов, d_кр.

Цель управления процессом - обеспечение d_кр = d_кр^зд.

Материальный баланс по всему веществу

Уравнение динамики:

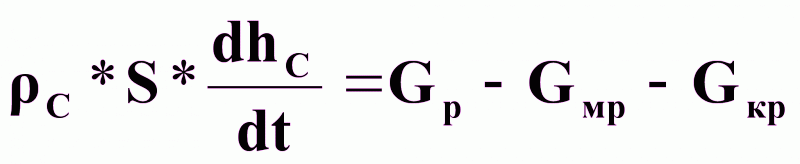(1).

Уравнение статики при :

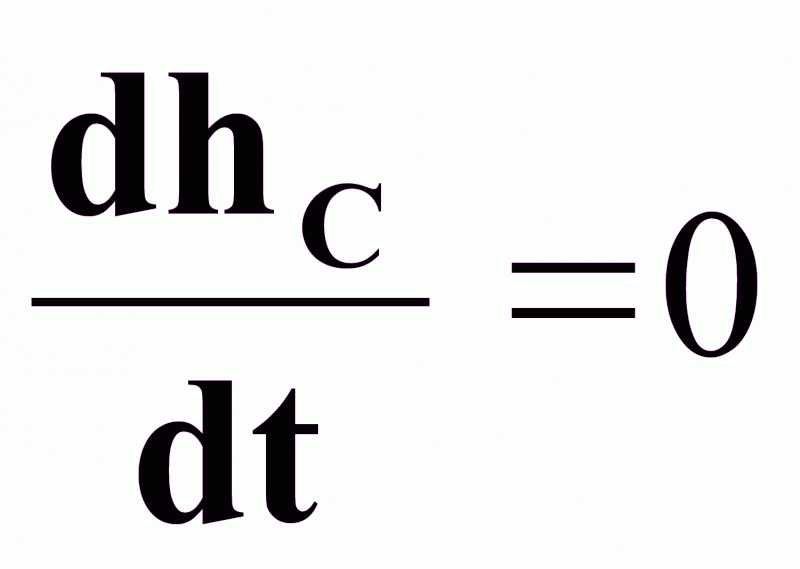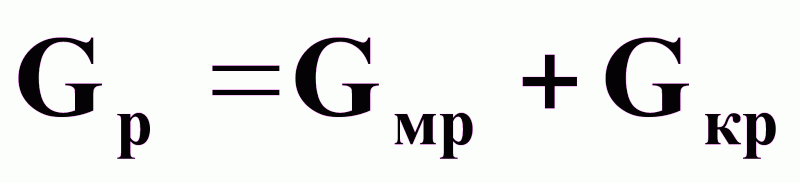(2).

Материальный баланс по кристаллизуемому веществу.

Уравнение динамики:

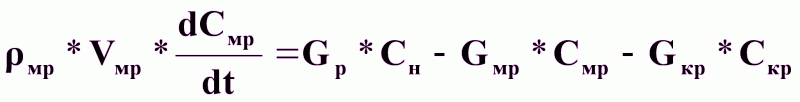(3).

Уравнение статики при :

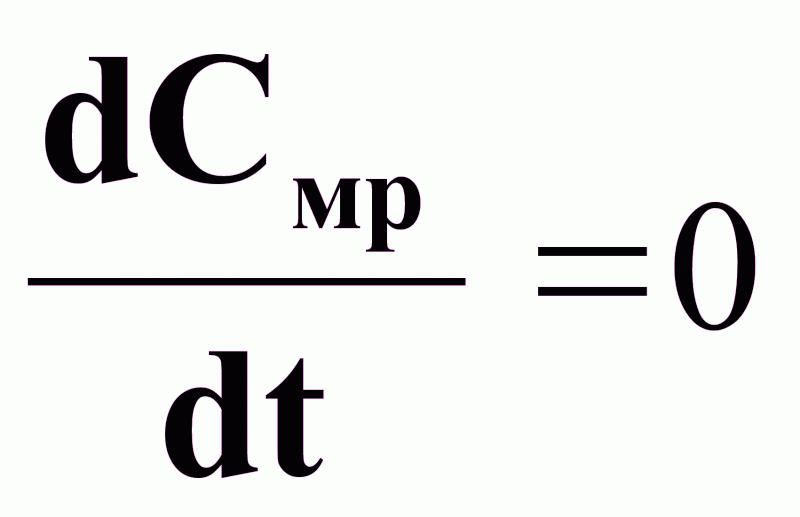(4).

• В уравнение (4) подставим выражение 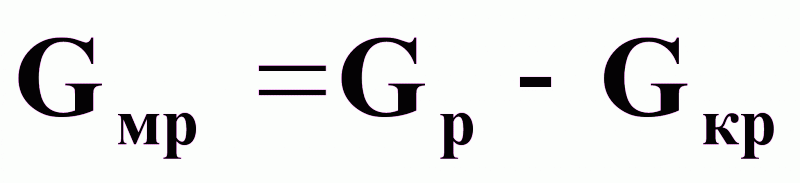из (2) и полагаем С_кр=1:

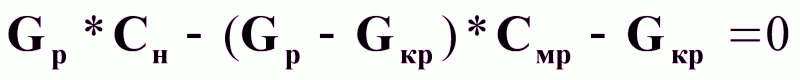(5).

• Из (5) выразим G_кр в явном виде:

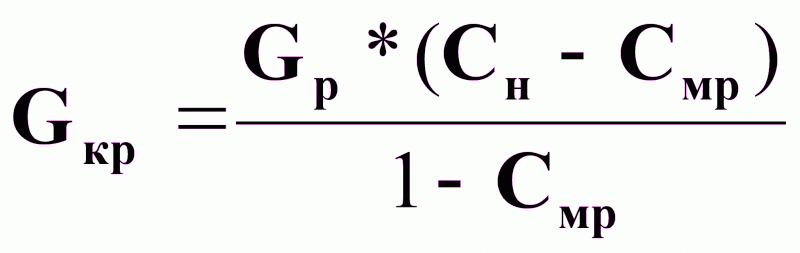(6).

• Выражение (6) представляет G_кр на основе материального баланса процесса кристаллизации.

• Но 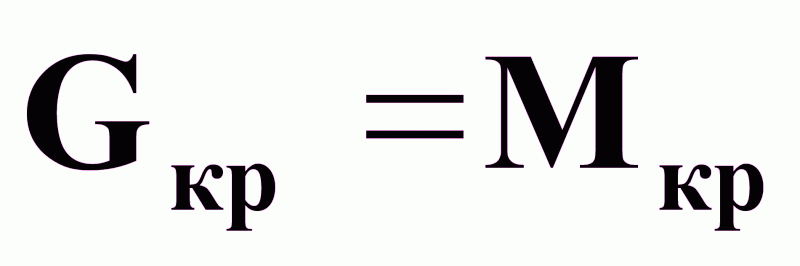, которое определяется на основе физики процесса массопередачи:

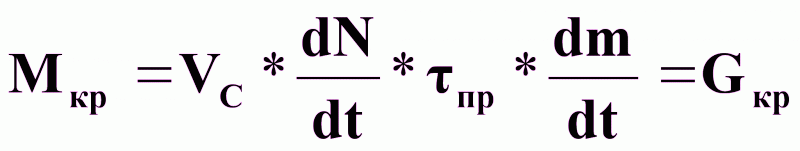(7),

где

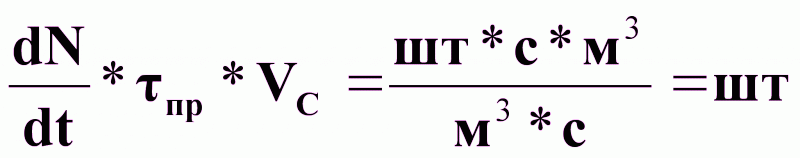- число кристаллов, которое образуется

за время _пр в объеме V_с;

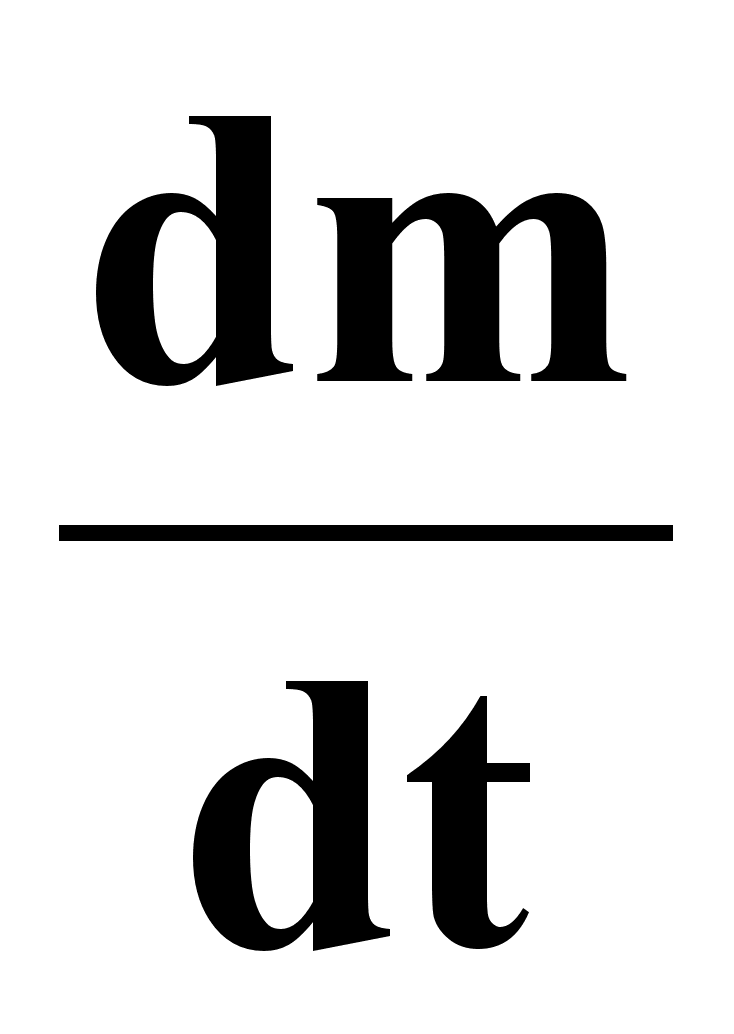- изменение массы одного кристалла в ед. времени, кг/с.

• Так как 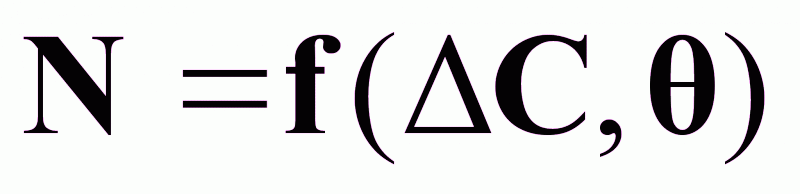и , а также 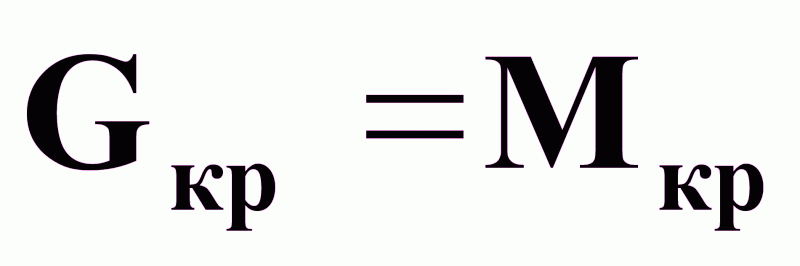, то на основе физики массопередачи можно считать:

.

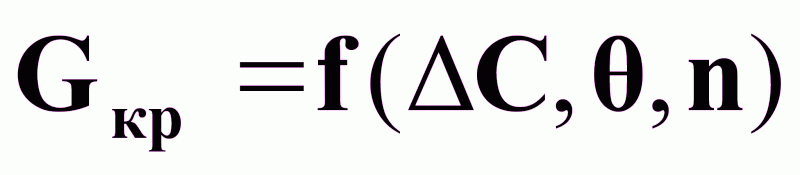• В целом, на основании (6) и (7) можно записать:

.

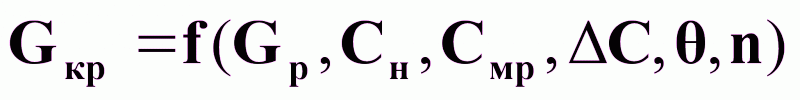Математическое описание для размера частиц.

• На основании диффузионной теории и правила Мак-Бена скорость роста кристаллов можно представить через радиус частиц:

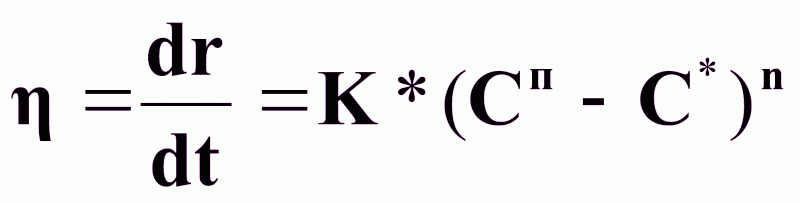(9),

где

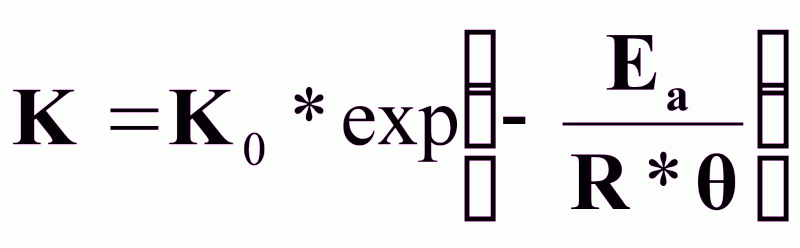(10);

r - радиус кристалла, м; t - время, с;

К, К₀ - константы, ;

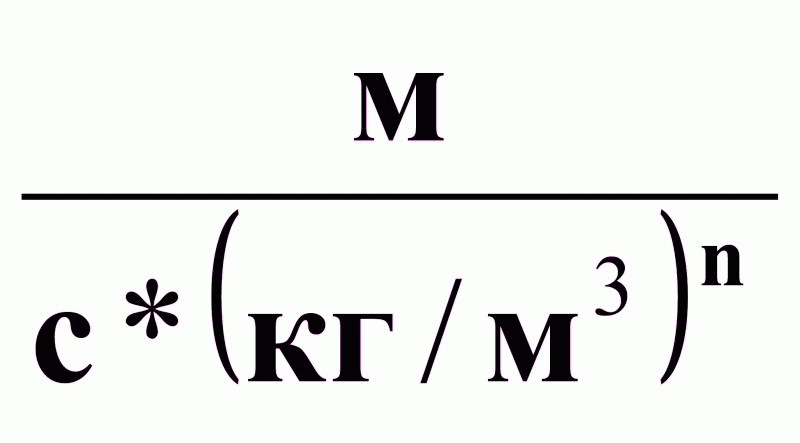С^п, С^* - концентрации пересыщенного и насыщенного растворов, кг/м³;

Е_а - энергия активации, кдж/кг;

• - температура, К;

R - универсальная газовая постоянная, кдж/кг*К.

• На основании (9) и (10) - диаметр кристалла можно представить:

.

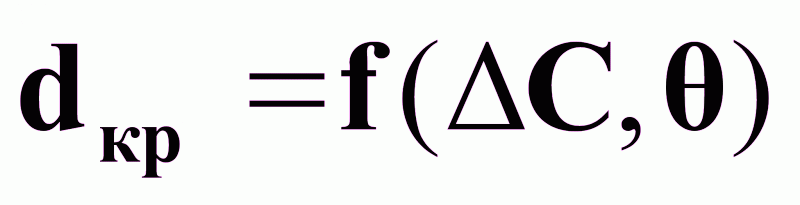• Если процесс кристаллизации вести при  = const = _зд и обеспечить С_н= const, то С^п и С^* будут предопределены, т.к. система имеет 2 степени свободы (s=2).

• Таким образом, d_кр=d_кр^зд можно обеспечить стабилизацией  при условии С_н= const.

Тепловой баланс процесса кристаллизации.

Уравнение динамики:

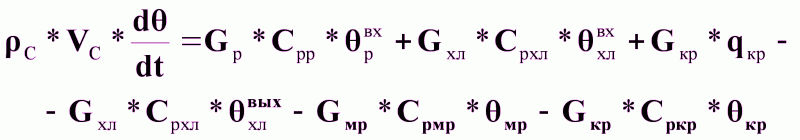(11).

Можно принять  = _мр = _кр = _с .

Уравнение статики при :

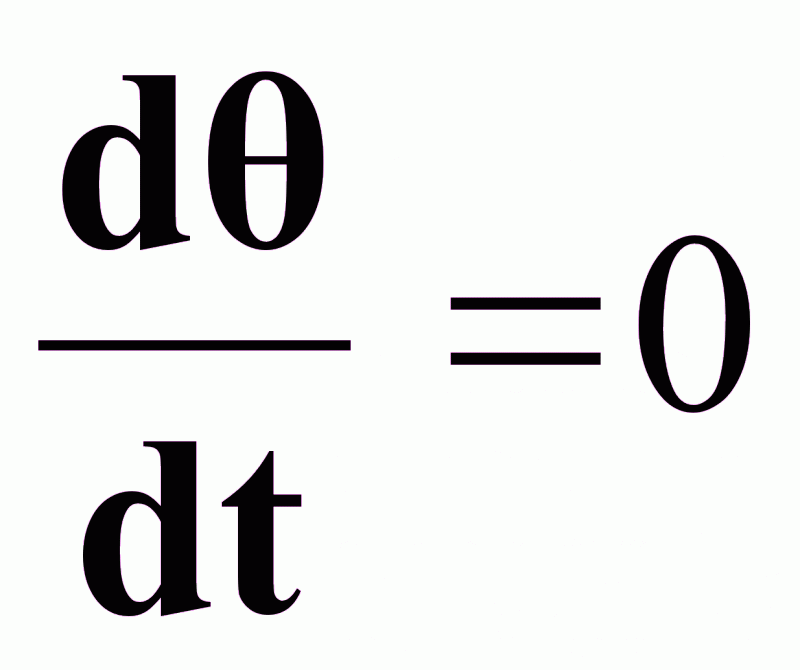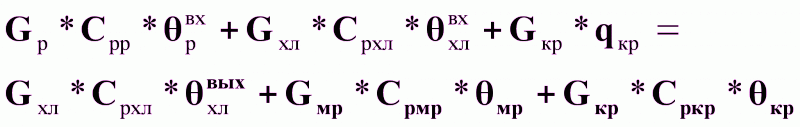(12).

• На основании (11) и (12) можно считать:

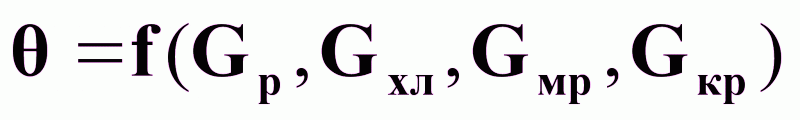
• Предпочтительное управляющее воздействие G_хл .

Информационная схема кристаллизатора

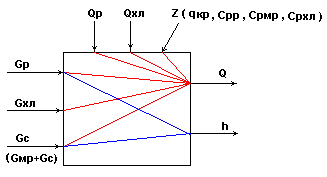
Рис.6.

• Основные регулируемые переменные: ;

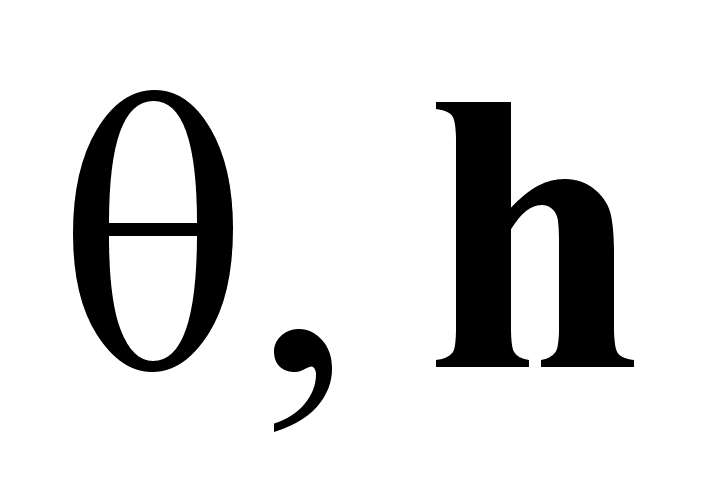• Возможные регулирующие воздействия:

• Возможные контролируемые возмущения:

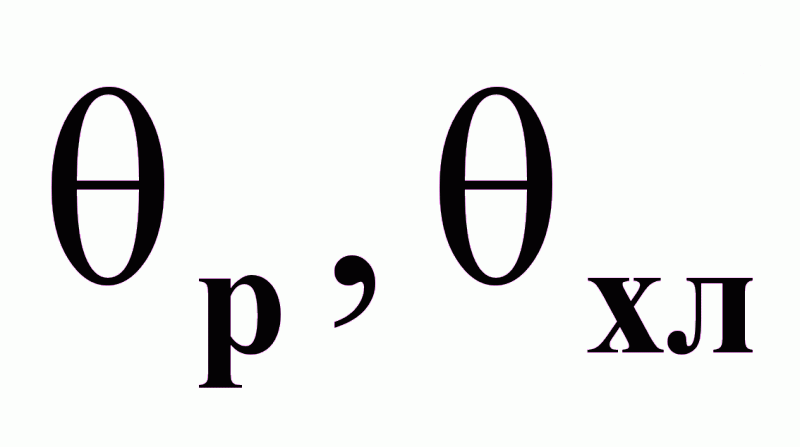
• Возможные неконтролируемые возмущения:

.

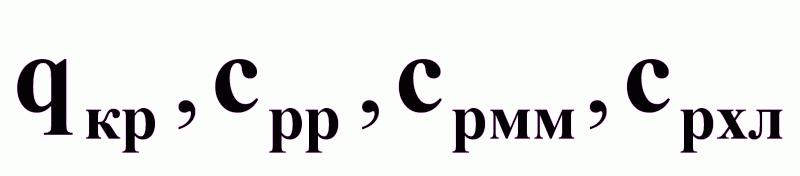• В целом, кристаллизатор является сложным многосвязным объектом.

Типовая схема автоматизации процесса кристаллизации

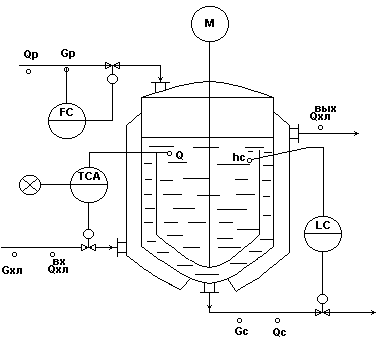
Рис.7.

1. Регулирование.

• Регулирование  в аппарате по подаче хладоагента G_хл - обеспечивает косвенное регулирование показателя эффективности процесса: = f (d_кр).

• Регулирование h по отбору маточного раствора G_мр - для обеспечения материального баланса по жидкой фазе.

• Стабилизация расхода исходного раствора G_р - для обеспечения заданной производительности установки.

2. Контроль.

• Расходы: .

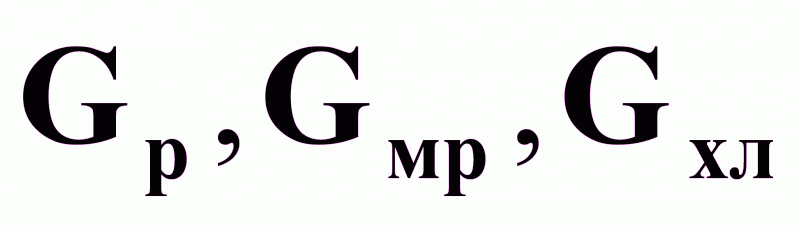• Температуры: .

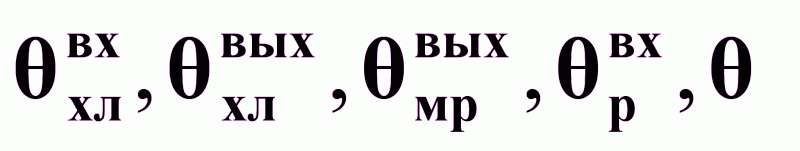• Уровень: h.

3. Сигнализация.

• Значительные отклонения температуры  от задания.

3. Материалы к лекции №11

Автоматизация процесса абсорбции

Равновесие в процессе абсорбции.

• Число степеней свободы для системы бинарный газ+жидкость:

S = k – f + 2=3-2+2=3.

• Переменные для данной системы: температура , давление Р; концентрации С.

• Равновесие такой системы при постоянных  и Р описывается законом Генри:

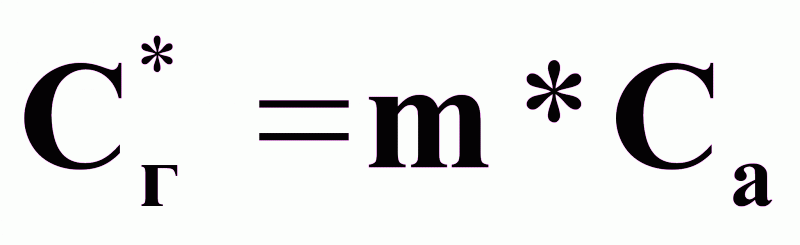(1),

где m - коэффициент распределения:

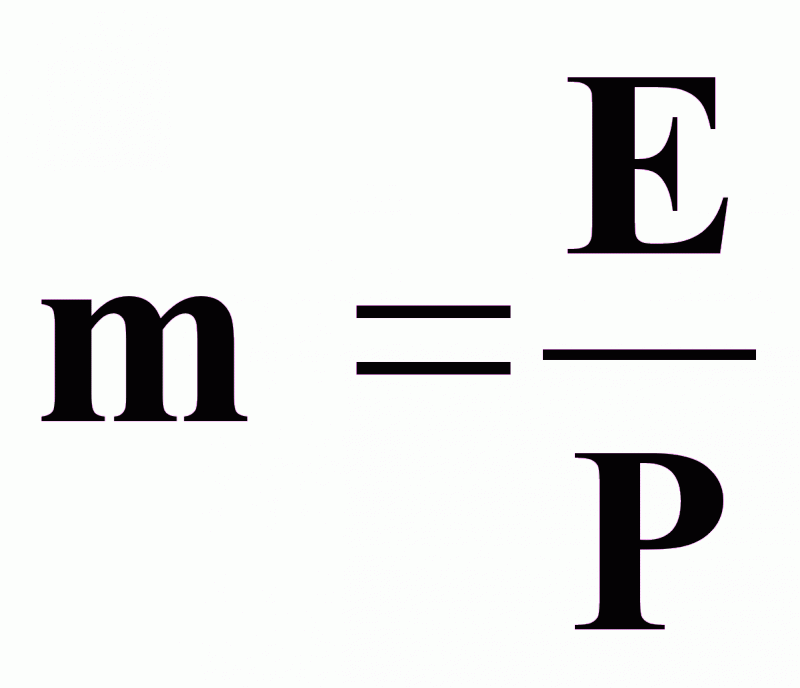(2),

где Е - константа Генри:

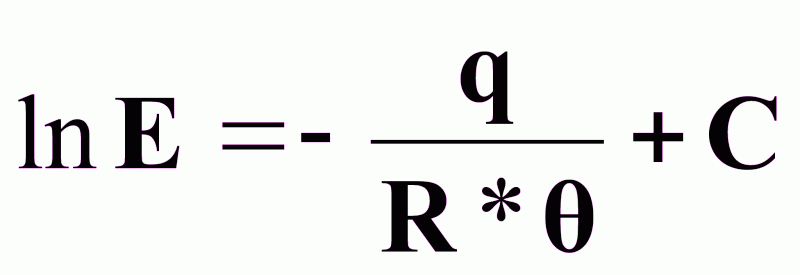(3),

где q - дифференциальная теплота растворения; R - универсальная газовая постоянная; С - константа.

• На основании (2) и (3) коэффициент распределения m зависит от P и  следующим образом: при Р, m ; при , Е  . m.

• Следовательно, растворимость газа в жидкости на основании (1), определяемая как: 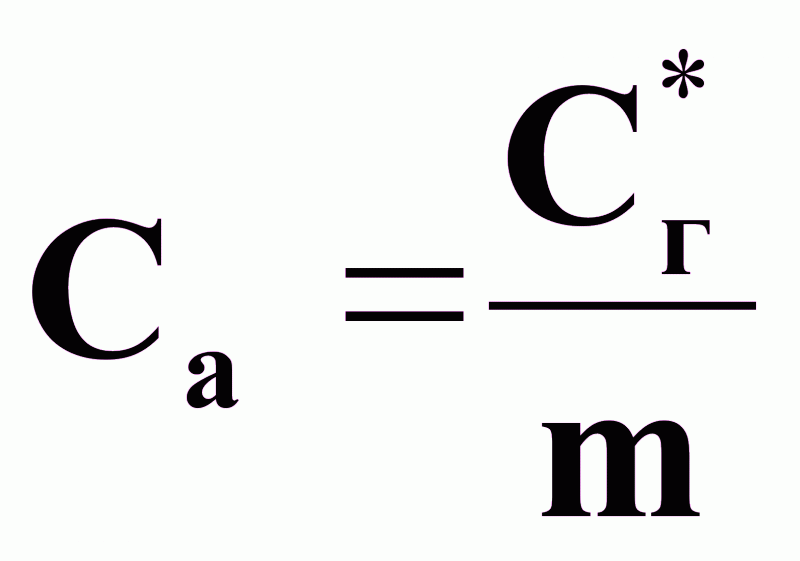, увеличивается с увеличением давления Р и уменьшением температуры .

Влияние Р и  на среднюю движущую силу процесса абсорбции.

(фазовые диаграммы при противотоке распределяющих веществ)

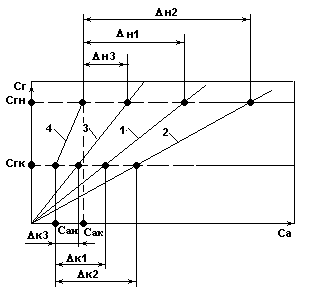
Рис.1.

1. При Р₁ и ₁ , Δ_ср1; 2 - При Р₂ > Р₁ , Δ_ср2 ; 3 - При ₃ > ₁ , Δ_ср3

Результаты анализа диаграмм:

• Δ_ср =f (, Р, с_гн , с_гк , с_ан , с_ак );

• Δ_ср2 > Δ_ср1 ; при Р→ Δ_ср ;

• Δ_ср3 < Δ_ср1 ; при → Δ_ср

Влияние направления движения потоков

на средние движущие силы процесса абсорбции.

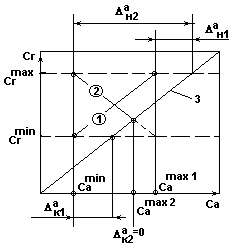
Рис.2а.

1. - рабочая линия процесса абсорбции при противотоке распределяющих веществ;

2. - рабочая линия процесса абсорбции при прямотоке распределяющих веществ;

3. - равновесная линия процесса абсорбции.

Движение распределяющих веществ противотоком.

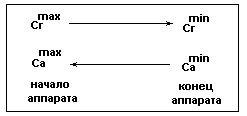
Рис.2б.

• С_а изменяется от С_а^min до С_а^max1 , ().

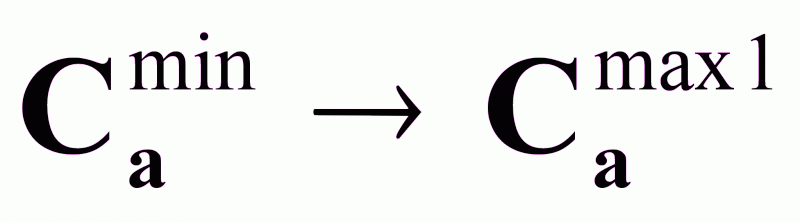• Движущая сила: .

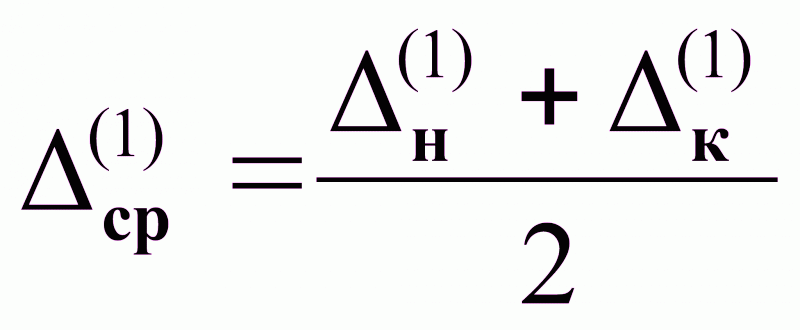Движение распределяющих веществ прямотоком.

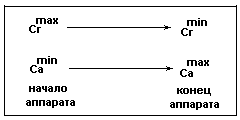
Рис.2в.

• С_а изменяется от С_а^min до С_а^max2 , ().

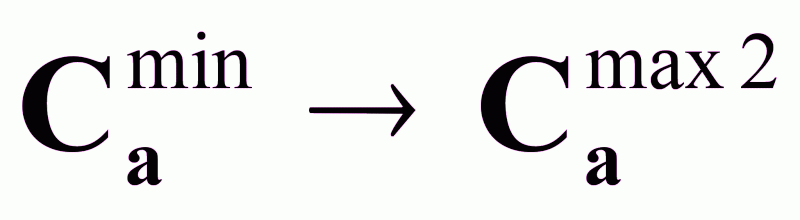• Движущая сила: .

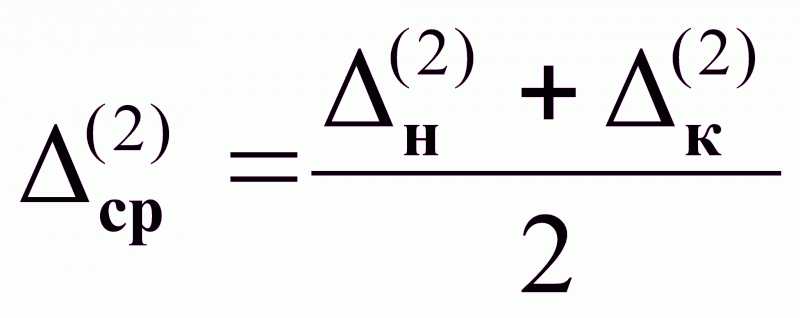• Выводы по характеристикам схем противотока и прямотока:

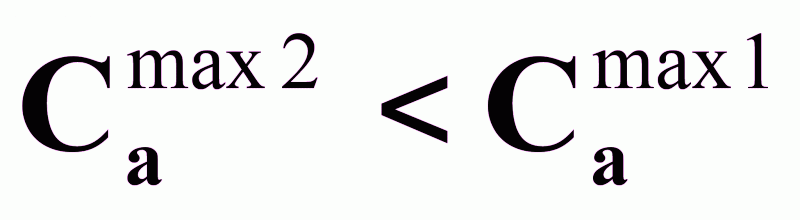1. - ; 2. - .

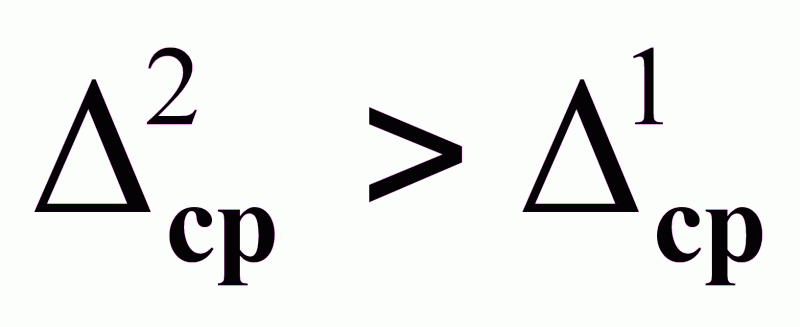Кинетика процесса абсорбции.

Уравнения массопередачи в процессе абсорбции:

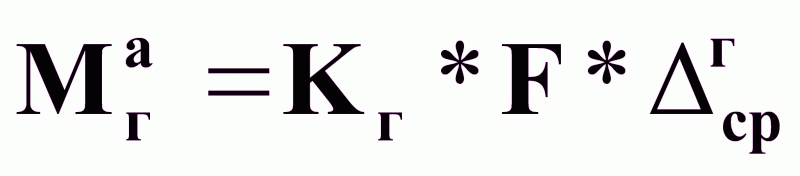
(4а),

или

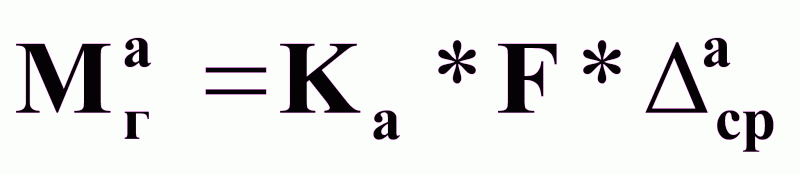(4б),

где

М_г^а - масса распределяемого компонента, переходящая из газа в абсорбент в единицу времени, кг/ч;

F - поверхность массопередачи м²;

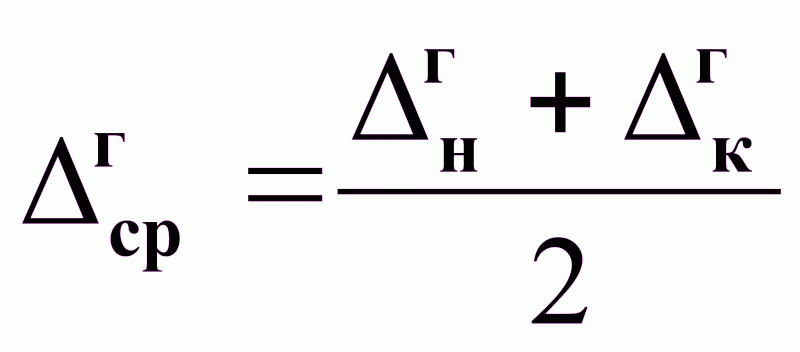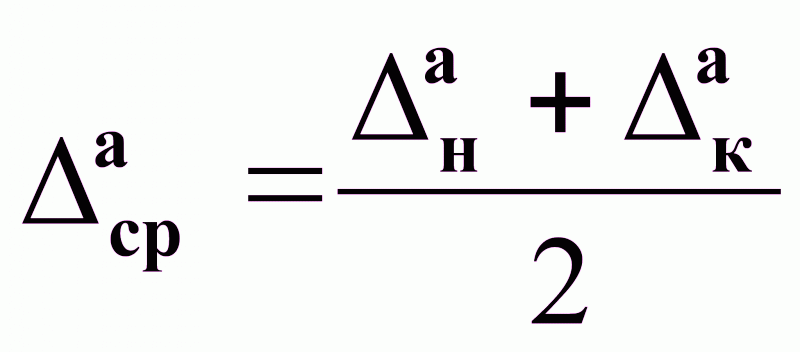и ;

и ;

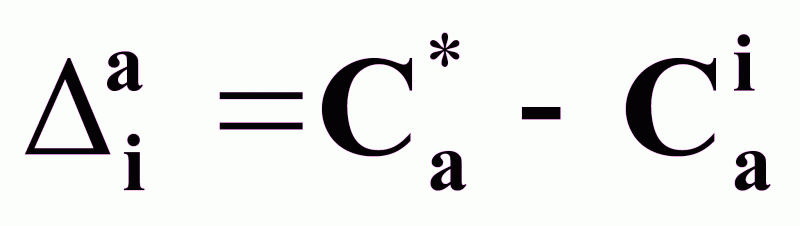К_г , К_а - коэффициенты массопередачи, ;

; ,

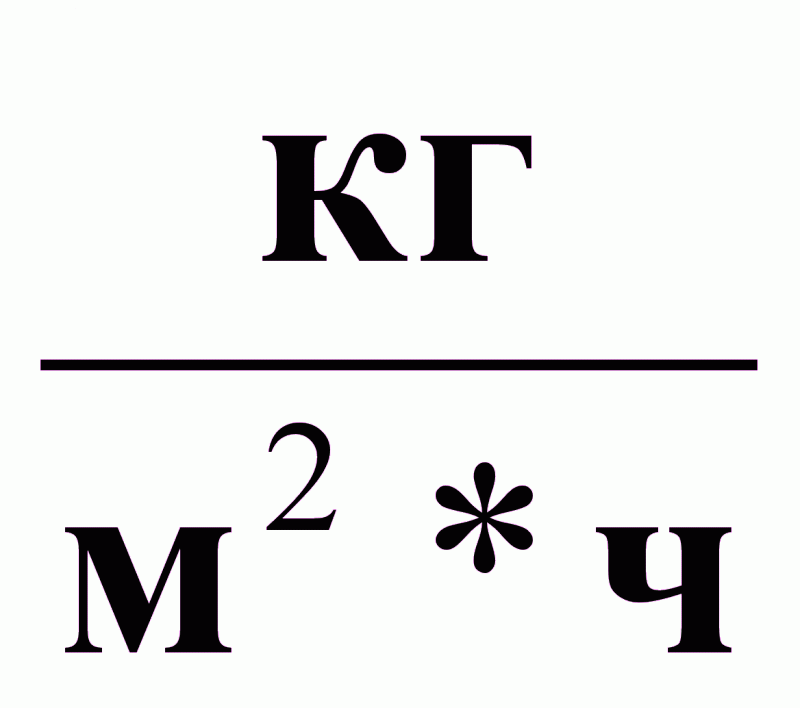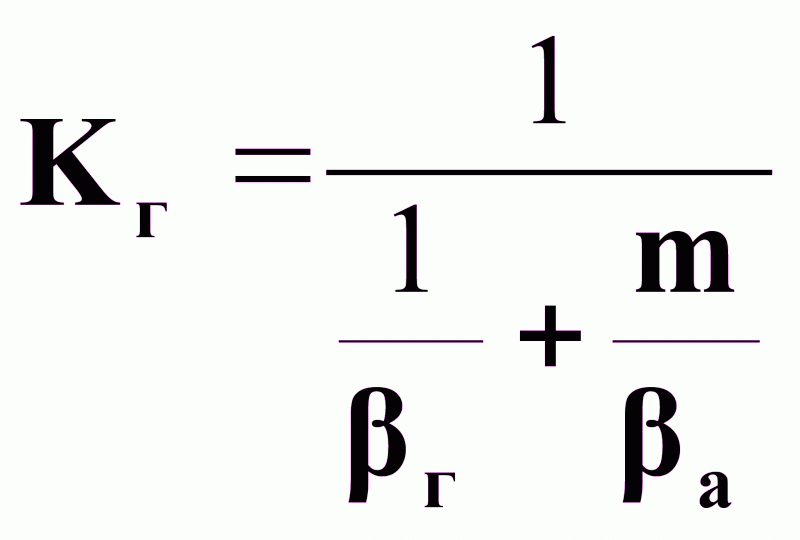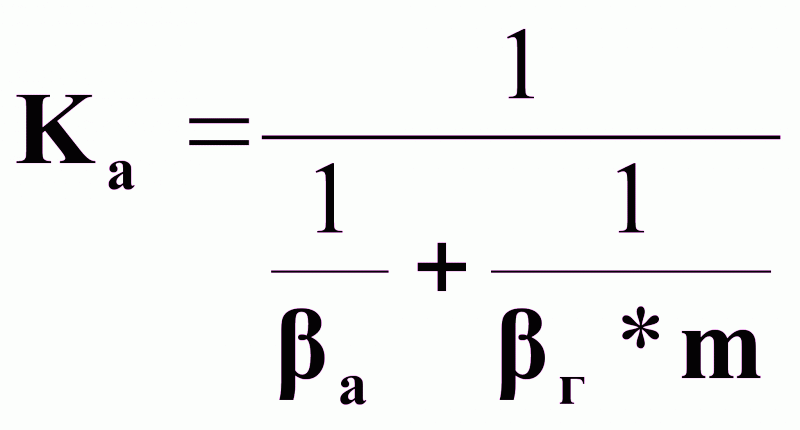где

_г - коэффициент массоотдачи от потока газа к поверхности контакта фаз, кг/(м² *ч);

_а - коэффициент массоотдачи от поверхности контакта фаз к потоку абсорбента, кг/(м² *ч).

Схема насадочного абсорбера.

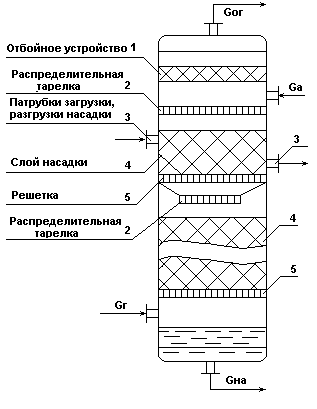
Рис.6.

Объект управления

Схема абсорбционной установки.

1, 2 – холодильники; 3 – абсорбционная насадочная колонна.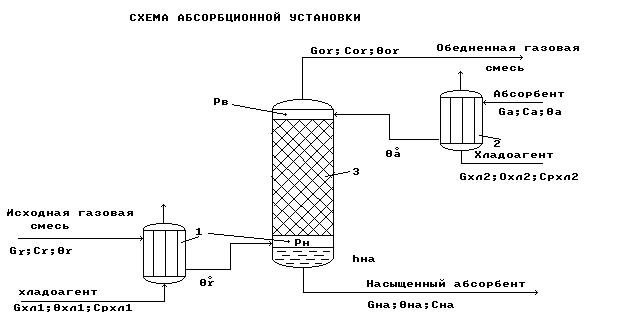

Рис.5.

Работа схемы.

Исходная газовая смесь G_г и абсорбент G_а в холодильниках 1 и 2 охлаждаются до заданных температур _г⁰ и _а⁰ и противотоком подаются в колонну 3.

В колонне 3 происходит извлечение целевого (распределяемого) компонента из исходной газовой смеси с помощью жидкого абсорбента.

В результате массообменного процесса между газовой и жидкой фазами получают:

• в низу колонны - насыщенный абсорбент G_на с концентрацией целевого (распределяемого) компонента с_на;

• в верху колонны - обедненную газовую смесь G_ог с концентрацией целевого (распределяемого) компонента с_ог .

Показатель эффективности процесса - концентрация распределяемого компонента в обедненной газовой смеси с_ог.

Цель управления - обеспечение с_ог = с_ог^зд на минимально возможном для данной установки значении.

Материальный баланс по целевому компоненту.

• Материальный баланс по целевому компоненту в газовой фазе.

Уравнение динамики:

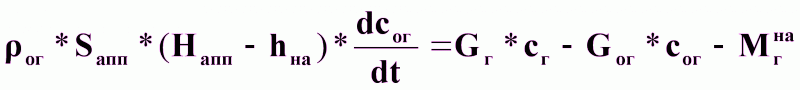(1),

где М_г^на - масса целевого компонента, переходящая из газовой фазы в жидкую в единицу времени, кг/ч.

Уравнение статики :

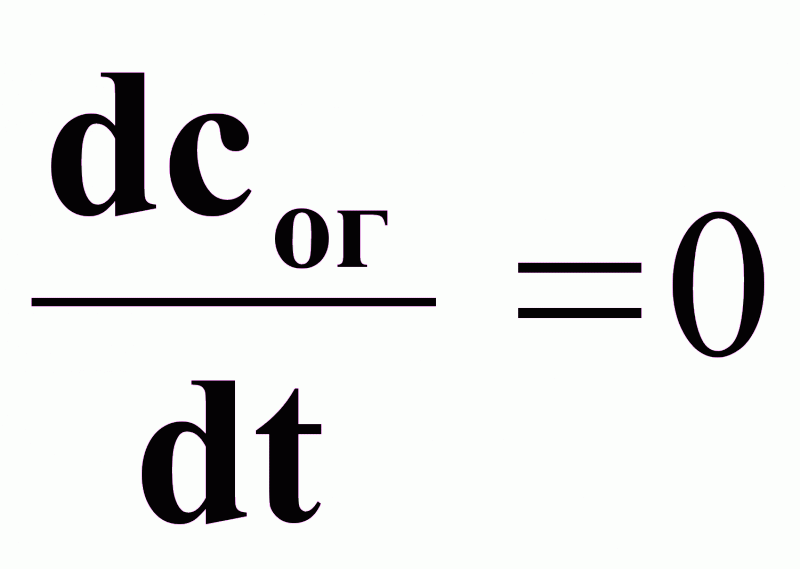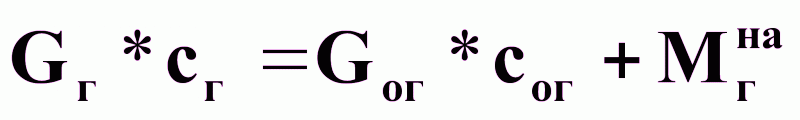(2).

Из выражений (1) и (2) следует, что: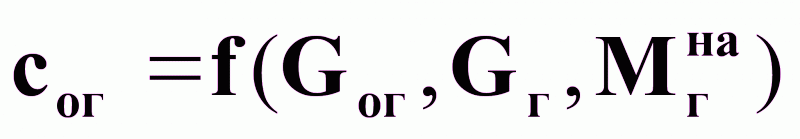 (3),

где М_г^на - определяется уравнением массопередачи.

• Материальный баланс по целевому компоненту в насыщенном абсорбенте.

Уравнение динамики:

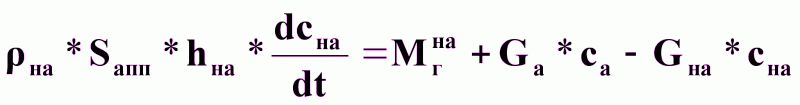(4).

Уравнение статики :

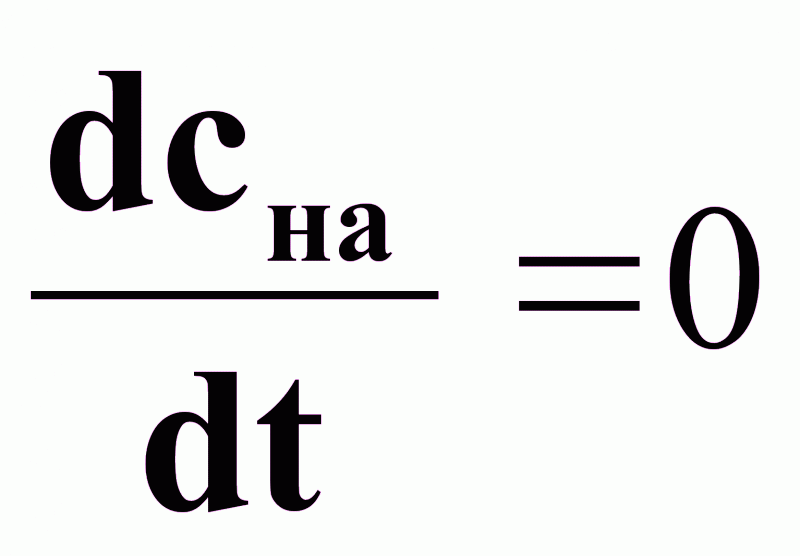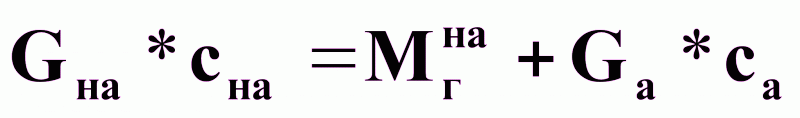(5).

Из выражений (4) и (5) следует, что: 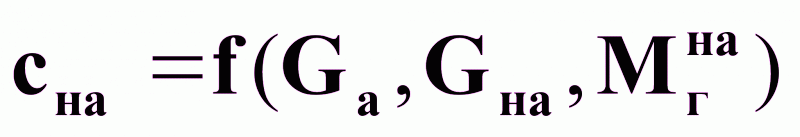(6),

где M_г^на - определяется уравнением массопередачи.

• Материальный баланс по общему количеству целевого компонента в процессе абсорбции.

Уравнение динамики:

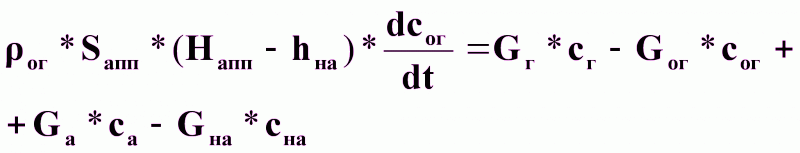
29-04-2015, 04:00